module 4 lesson 22 grade 5 homework

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Eureka Math Grade 5 Module 4 Lesson 22 Answer Key

Engage ny eureka math 5th grade module 4 lesson 22 answer key, eureka math grade 5 module 4 lesson 22 problem set answer key.

Question 1. Solve for the unknown. Rewrite each phrase as a multiplication sentence. Circle the scaling factor and put a box around the number of meters. a. \(\frac{1}{2}\) as long as 8 meters = ______ meter(s)

Answer: 4 meters.

Explanation: Given that \(\frac{1}{2}\) as long as 8 meters which is \(\frac{1}{2}\) × 8 = 4 meters.

b. 8 times as long as \(\frac{1}{2}\) meter = _______ meter(s)

Explanation: Given that \(\frac{1}{2}\) meter is 8 times as long, so 8 × \(\frac{1}{2}\) which is 4 meters.

Question 2. Draw a tape diagram to model each situation in Problem 1, and describe what happened to the number of meters when it was multiplied by the scaling factor. a. Answer: The scaling factor is less than 1, so the number of meters decreases.

b. Answer: The scaling factor is greater than 1, so the number of meters increased.

Question 3. Fill in the blank with a numerator or denominator to make the number sentence true. a. 7 × \(\frac{}{4}\) < 7

Answer: 7 × \(\frac{}{4}\) < 7.

Explanation: Given that 7 × \(\frac{}{4}\) < 7, so here in the numerator we will place a number that is less than 4. So we will place 3 in the numerator which will be 7 × \(\frac{3}{4}\) < 7.

b. \(\frac{7}{}\) × 15 > 15

Answer: \(\frac{7}{2}\) × 15 > 15

Explanation: Given that \(\frac{7}{2}\) × 15 > 15, so here in the denominator we will place a number that is less than 7. So we will place 2 in the denominator which will be \(\frac{7}{2}\) × 15 > 15.

c. 3 × \(\frac{}{5}\) = 3

Answer: 3 × \(\frac{5}{5}\) = 3

Explanation: Given that 3 × \(\frac{}{5}\) = 3, so to justify the answer we will place 5 in the numerator which is 3 × \(\frac{5}{5}\) = 3.

Question 4. Look at the inequalities in each box. Choose a single fraction to write in all three blanks that would make all three number sentences true. Explain how you know.

Answer: \(\frac{5}{2}\).

Answer: \(\frac{1}{2}\).

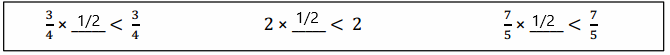
Question 5. Johnny says multiplication always makes numbers bigger. Explain to Johnny why this isn’t true. Give more than one example to help him understand.

Answer: 4 times 0.5 equals 2.

Explanation: Given that Johnny says multiplication always makes numbers bigger which is not true because if we multiply any number by a decimal number, we will make it smaller. Because if we multiply a number by something less than one, we will get something less than itself. This also works if you multiply a number by a fraction. For example, 4 times 0.5 equals 2 because you are getting half of the original number which is 4.

Question 6. A company uses a sketch to plan an advertisement on the side of a building. The lettering on the sketch is \(\frac{3}{4}\) inch tall. In the actual advertisement, the letters must be 34 times as tall. How tall will the letters be on the building?

Answer: The letters on the building would be 25 \(\frac{1}{2}\) inch.

Explanation: Given that a company uses a sketch to plan an advertisement on the side of a building and lettering on the sketch is \(\frac{3}{4}\) inch tall and the letters must be 34 times as tall. So to find the height of the building, we will multiply 34 × \(\frac{3}{4}\) inch and the height of the letters on the building which is 34 × \(\frac{3}{4}\) inch = \(\frac{104}{4}\) inch = \(\frac{51}{2}\) inch = 25 \(\frac{1}{2}\) inch. Therefore the letters on the building would be 25 \(\frac{1}{2}\) inch.

Question 7. Jason is drawing the floor plan of his bedroom. He is drawing everything with dimensions that are \(\frac{1}{12}\) of the actual size. His bed measures 6 ft by 3 ft, and the room measures 14 ft by 16 ft. What are the dimensions of his bed and room in his drawing?

Answer: The dimensions of his room in his drawing are 1 \(\frac{1}{3}\) by1 \(\frac{1}{6}\) ft, The dimensions of his bed in his drawing are \(\frac{1}{2}\) ft by \(\frac{1}{4}\) ft.

Explanation: Given that Jason is drawing the floor plan of his bedroom and he is drawing everything with dimensions that are \(\frac{1}{12}\) of the actual size and his bed measures 6 ft by 3 ft, and the room measures 14 ft by 16 ft. So the dimensions of his room in his drawing are \(\frac{1}{12}\) of 16 ft and \(\frac{1}{12}\) of 14 ft which is = \(\frac{1}{12}\) × 16 = \(\frac{4}{3}\) = 1 \(\frac{1}{3}\) \(\frac{1}{12}\) of 14 ft = \(\frac{1}{12}\) × 14 ft = \(\frac{7}{6}\) = 1 \(\frac{1}{6}\) ft So the dimensions of his room in his drawing are 1 \(\frac{1}{3}\) by1 \(\frac{1}{6}\) ft. For his bed in his drawing are \(\frac{1}{12}\) of 6 ft by \(\frac{1}{12}\) of 3 which is = \(\frac{1}{12}\) × 6 = \(\frac{1}{2}\) ft \(\frac{1}{12}\) of 3 = \(\frac{1}{12}\) × 3 = \(\frac{1}{4}\) ft. So the dimensions of his bed in his drawing are \(\frac{1}{2}\) ft by \(\frac{1}{4}\) ft.

Eureka Math Grade 5 Module 4 Lesson 22 Exit Ticket Answer Key

Fill in the blank to make the number sentences true. Explain how you know. a. \(\frac{}{3}\) × 11 ˃ 11

Answer: \(\frac{4}{3}\) × 11 ˃ 11.

Explanation: Given that \(\frac{}{3}\) × 11 ˃ 11, so here in the numerator we will place a number that is greater than 3. So we will place 4 in the numerator which will be \(\frac{4}{3}\) × 11 ˃ 11.

b. 5 × \(\frac{}{8}\) ˂ 5

Answer: 5 × \(\frac{5}{8}\) ˂ 5.

Explanation: Given that 5 × \(\frac{}{8}\) ˂ 5, so here in the numerator we will place a number that is less than 8. So we will place 5 in the numerator which will be 5 × \(\frac{5}{8}\) ˂ 5.

c. 6 × \(\frac{2}{}\) = 6

Answer: 6 × \(\frac{2}{2}\) = 6

Explanation: Given that 6 × \(\frac{2}{2}\) = 6, so to justify the answer we will place 2 in the numerator which is 6 × \(\frac{2}{2}\) = 6

Eureka Math Grade 5 Module 4 Lesson 22 Homework Answer Key

Question 1. Solve for the unknown. Rewrite each phrase as a multiplication sentence. Circle the scaling factor and put a box around the number of meters. a. \(\frac{1}{3}\) as long as 6 meters = ______ meter(s)

Answer: 2 meters.

Explanation: Given that \(\frac{1}{3}\) as long as 6 meters which is \(\frac{1}{3}\) × 6 = 2 meters.

b. 6 times as long as \(\frac{1}{3}\) meter = ______ meter(s)

Explanation: Given that \(\frac{1}{3}\) meter is 6 times as long, so 6 × \(\frac{1}{3}\) which is2 meters.

Question 2. Draw a tape diagram to model each situation in Problem 1, and describe what happened to the number of meters when it was multiplied by the scaling factor. a.

Answer: The scaling factor is less than 1, so the number of meters decreases.

Answer: The scaling factor is greater than 1, so the number of meters increased.

Explanation: The scaling factor is greater than 1, so the number of meters increased.

Question 3. Fill in the blank with a numerator or denominator to make the number sentence true. a. 5 × \(\frac{}{3}\) ˃ 5

Answer: 5 × \(\frac{2}{3}\) ˃ 5.

Explanation: Given that 5 × \(\frac{4}{3}\) ˃ 5, so here in the numerator, we will place a number that is greater than 3. So we will place 4 in the numerator which will be 5 × \(\frac{4}{3}\) ˃ 5.

b. \(\frac{6}{}\) × 12 ˂ 12

Answer: \(\frac{6}{}\) × 12 ˂ 12.

Explanation: Given that \(\frac{6}{7}\) × 12 ˂ 12, so here in the numerator, we will place a number that is greater than 6. So we will place 7 in the numerator which will be \(\frac{6}{7}\) × 12 ˂ 12.

c. 4 × \(\frac{}{5}\) = 4

Answer: 4 × \(\frac{5}{5}\) = 4

Explanation: Given that 4 × \(\frac{5}{5}\) = 4, so to justify the answer we will place 5 in the numerator which is 4 × \(\frac{5}{5}\) = 4.

Answer: \(\frac{5}{4}\).

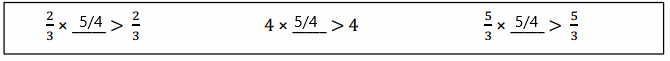
Question 5. Write a number in the blank that will make the number sentence true. a. 3 × _____ ˂ 1

Answer: 3 × \(\frac{1}{4}\) < 1.

Explanation: To make the number sentence true we will place the number which is less than \(\frac{1}{3}\), so we will place \(\frac{1}{4}\) which will be less than 1. So the expression will be 3 × \(\frac{1}{4}\) < 1.

b. Explain how multiplying by a whole number can result in a product less than 1.

Answer: When a positive whole number is multiplied by a fraction between 0 and 1, the product is less than the whole number. When a number greater than 1 is multiplied by a number greater than 1, the product is greater than both numbers.

Question 6. In a sketch, a fountain is drawn \(\frac{1}{4}\) yard tall. The actual fountain will be 68 times as tall. How tall will the fountain be?

Answer: The actual height of the fountain is 17 yards.

Explanation: Given that a fountain is drawn \(\frac{1}{4}\) yard tall and the actual fountain will be 68 times as tall. So the actual height of the fountain is \(\frac{1}{4}\) × 68 which is 17 yards.

Question 7. In blueprints, an architect’s firm drew everything \(\frac{1}{24}\) of the actual size. The windows will actually measure 4 ft by 6 ft and doors measure 12 ft by 8 ft. What are the dimensions of the windows and the doors in the drawing?

Answer: The dimensions of the windows are 2 in by 3 in. The dimensions of the windows are 6 in by 4 in.

Explanation: Given that an architect’s firm drew everything \(\frac{1}{24}\) of the actual size and the windows will actually measure 4 ft by 6 ft, so the dimensions of the length of the windows are \(\frac{1}{24}\) × 4 which is \(\frac{1}{6}\) ft, so in inch, it will be \(\frac{1}{6}\) × 12 which is 2 in. And the width of the windows is \(\frac{1}{24}\) × 6 which is \(\frac{1}{4}\), so in inch, it will be \(\frac{1}{4}\) × 12 which is 3 in. So the dimensions of the windows are 2 in by 3 in. Given that the measures of the door are 12 ft by 8 ft, so the dimensions of the length of the doors are \(\frac{1}{24}\) × 12 which is \(\frac{1}{2}\) ft, so in inch, it will be \(\frac{1}{2}\) × 12 which is 6 in. And the width of the windows is \(\frac{1}{24}\) × 8 which is \(\frac{1}{3}\), so in inch, it will be \(\frac{1}{3}\) × 12 which is 4 in.