problem solving strategy look for a pattern

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Problem Solving by Finding a Pattern

One important math concept that children begin to learn and apply in elementary school is reading and using a table. This is essential knowledge, because we encounter tables of data all the time in our everyday lives! But it’s not just important that kids can read and answer questions based on information in a table, it’s also important that they know how to create their own table and then use it to solve problems, find patterns, graph equations, and so on. And while some may think of these as two different things, I think problem solving by making a table and finding a pattern go hand in hand!

This is such a useful math problem solving strategy! Kids can get so overwhelmed by math word problems, but helping them organize the information in a table and then find a pattern can make things easier!

–>Pssst! Do your kids need help making sense of and solving word problems? You might like this set of editable word problem solving templates ! Use these with any grade level, for any type of word problem :

Finding Patterns in Math Problems:

So when should kids use problem solving by finding a pattern ? Well, when the problem gives a set of data, or a pattern that is continuing and can be arranged in a table, it’s good to consider looking for the pattern and determining the “rule” of the pattern.

As I mentioned when I discussed problem solving by making a list , finding a pattern can be immensely helpful and save a lot of time when working on a word problem. Sometimes, however, a student may not recognize the pattern right away, or may get bogged down with all the details of the question.

Setting up a table and filling in the information given in the question is a great way to organize things and provide a visual so that the “rule” of the pattern can be determined. The “rule” can then be used to find the answer to the question. This removes the tedious work of completing a table, which is especially nice if a lot of computation is involved.

But a table is also great for kids who struggle with math, because it gives them a way to get to the solution even if they have a hard time finding the pattern, or aren’t confident that they are using the “rule” correctly.

Because even though using a known pattern can save you time, and eliminate the need to fill out the entire table, it’s not necessary. A student who is unsure could simply continue filling out their table until they reach the solution they’re looking for.

Helping students learn how to set up a table is also helpful because they can use it to organize information (much like making a list) even if there isn’t a pattern to be found, because it can be done in a systematic way, ensuring that nothing is left out.

If your students are just learning how to read and create tables, I would suggest having them circle their answer in the table to show that they understood the question and knew where in the table to find the answer.

If you have older students, encourage them to find a pattern in the table and explain it in words , and then also with mathematical symbols and/or an equation. This will help them form connections and increase number sense. It will also help them see how to use their “rule” or equation to solve the given question as well as make predictions about the data.

It’s also important for students to consider whether or not their pattern will continue predictably . In some instances, the pattern may look one way for the first few entries, then change, so this is important to consider as the problems get more challenging.

There are tons of examples of problems where creating a table and finding a pattern is a useful strategy, but here’s just one example for you:

Ben decides to prepare for a marathon by running ten minutes a day, six days a week. Each week, he increases his time running by two minutes per day. How many minutes will he run in week 8?

Included in the table is the week number (we’re looking at weeks 1-8), as well as the number of minutes per day and the total minutes for the week. The first step is to fill in the first couple of weeks by calculating the total time.

Making a table and finding a pattern is an excellent math problem solving strategy! This is a great example!

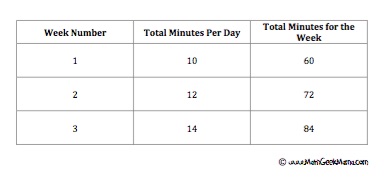
Once you’ve found weeks 1-3, you may see a pattern and be able to calculate the total minutes for week 8. For example, in this case, the total number of minutes increases by 12 each week, meaning in week 8 he will run for 144 minutes.

If not, however, simply continue with the table until you get to week 8, and then you will have your answer.

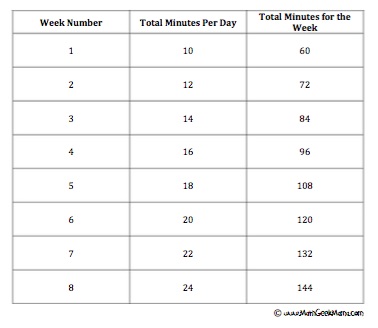
I think it is especially important to make it clear to students that it is perfectly acceptable to complete the entire table (or continue a given table) if they don’t see or don’t know how to use the pattern to solve the problem.

I was working with a student once and she was given a table, but was then asked a question about information not included in that table . She was able to tell me the pattern she saw, but wasn’t able to correctly use the “rule” to find the answer. I insisted that she simply extend the table until she found what she needed. Then I showed her how to use the “rule” of the pattern to get the same answer.

I hope you find this helpful! Looking for and finding patterns is such an essential part of mathematics education! If you’re looking for more ideas for exploring patterns with younger kids, check out this post for making patterns with Skittles candy .

And of course, don’t miss the other posts in this Math Problem Solving Series:

Problem Solving by Solving an Easier Problem
Problem Solving by Drawing a Picture
Problem Solving by Working Backwards
Problem Solving by Making a List

One Comment

I had so much trouble spotting patterns when I was in school. Fortunately for her, my daughter rocks at it! This technique will be helpful for her when she’s a bit older! #ThoughtfulSpot

Comments are closed.

Valentine’s Day STEM: Build a Tower with Conversation Hearts

$8 Reasons Making Mistakes in Math is a GOOD Thing!$

8 Reasons Making Mistakes in Math is a GOOD Thing!

Weekly Math Freebie Round Up!

Teach Kids to Be Curious Like Einstein

September Problem of the Day Calendar

Add & Subtract Decimals on a Number Line {FREE Printable Number Lines!}

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Pattern Problem Solving: Teach Students to Find a Pattern in Math Problems

Pattern analysis is a critical 21st century skill.

Need more tips and tricks for teaching math? You can find them in our math resources center .

Pattern problem solving

In this article, we’ll delve into the concept of pattern problem solving, a fundamental mathematical strategy that involves the identification of repeated sequences or elements to solve complex problems.

This method is instrumental in enhancing logical thinking and mathematical comprehension among students. Let's explore how this works, why it's important, and how to teach this critical skill effectively.

Math teacher teaches problem solving. pattern problem solving.

What is pattern problem solving?

Pattern problem solving is a mathematical strategy in which students look for patterns in data to solve a problem. To find a pattern, students search for repeated items, numbers, or series of events.

The following problem can be solved by finding the pattern:

There are 1000 lockers in a high school with 1000 students. The first student opens all 1000 lockers; next, the second student closes lockers 2, 4, 6, 8, 10, and so on up to locker 1000; the third student changes the state (opens lockers that are closed, closes lockers that are open) of lockers 3, 6, 9, 12, 15, and so on; the fourth student changes the state of lockers 4, 8, 12, 16, and so on. This continues until every student has had a turn. How many lockers will be open at the end?

For the answer, visit The Locker Problem from the Math Doctors

Why is pattern problem solving important?

Pattern problem solving is an important strategy for students as it encourages them to observe and understand patterns in data, which is a critical aspect of mathematical and logical thinking.

This strategy allows students to predict future data points or behaviors based on existing patterns. It helps students understand the inherent structure of data sets and mathematical problems, making them easier to solve.

Pattern recognition also aids in the understanding of multiplication facts, for example, recognizing that 4 x 7 is the same as 7 x 4. Overall, pattern problem solving fosters analytical thinking, problem-solving skills, and a deeper understanding of mathematics.

Boy solves math problem in class. pattern problem solving.

How to teach students to find the pattern in a math problem (using an example)

In the upcoming section, we will break down the steps on how to find a pattern in a math problem effectively. We will use a practical example to illustrate each step and provide helpful teaching tips throughout the process.

The goal is to offer a clear and comprehensible guide for educators teaching students about pattern problem solving in math.

Sample question: If you build a four-sided pyramid using basketballs and don't count the bottom as a side, how many balls will there be in a pyramid that has six layers?

Helpful teaching tip: Use cooperative learning groups to find solutions to the above problem. Cooperative learning groups help students verbalize their thinking, brainstorm ideas, discuss options, and justify their positions. After finding a solution, each group can present it to the class, explaining how they reached their solution and why they think it is correct. Or, students can explain their solutions in writing, and the teacher can display the solutions. Then students can circulate around the room to read each group's solution.

1. Ensure students understand the problem

Demonstrate that the first step to solving a problem is understanding it. This involves identifying the key pieces of information needed to find the answer. This may require students to read the problem several times or put the problem into their own words.

Sometimes you can solve a problem simply through pattern recognition, but more often you must extend the pattern to find the solution. Making a number table will help you see the pattern more clearly.

In this problem, students understand:

The top layer will have one basketball. I need to find how many balls there will be in each layer of a pyramid, from the first to the sixth. I need to find how many basketballs will be in the entire pyramid.

2. Choose a pattern problem solving strategy

To successfully find a pattern, you need to be sure that the pattern will continue.

Have students give reasons why they think the pattern is predictable and not based on probability. Problems that are solved most easily by finding a pattern include those that ask students to extend a sequence of numbers or to make a prediction based on data.

In this problem, students may also choose to make a table or draw a picture to organize and represent their thinking.

3. Solve the problem

Start with the top layer of the pyramid, one basketball. Determine how many balls must be under that ball to make the next layer or a pyramid. Let students use manipulatives if needed— they can use manipulatives of any kind, from coins to cubes to golf balls. Let students also draw pictures to help solve the problem, if needed.

If your students are in groups, you may want to have each group use a different manipulative and then compare their solutions. This will help you understand if different manipulatives affect the solution.

Helpful teaching tip: If students are younger, solve this problem with only three layers.

If it helps to visualize the pyramid, use manipulatives to create the third layer. Record the number and look for a pattern. The second layer adds 3 basketballs and the next adds 5 basketballs. Each time you add a new layer, the number of basketballs needed to create that layer increases by 2.

1 1 + 3 = 4 4 + 5 = 9

Continue until six layers are recorded. Once a pattern is found, students might not need to use manipulatives. 9 + 7 = 16

16 + 9 = 25 25 + 11 = 36

Then add the basketballs used to make all six layers.

The answer is 91 balls .

Look at the list to see if there is another pattern. The number of balls used in each level is the square of the layer number. So the 10th layer would have 10 x 10 = 100 balls .

4. Check your students' answers

Read the problem again to be sure the question was answered:

Yes, I found the total number of basketballs in the six-layer pyramid.

Also check the math to be sure it’s correct:

1 + 4 + 9 + 16 + 25 +36 = 91

Determine if the best strategy was chosen for this problem, or if there was another way to solve the problem:

Finding a pattern was a good way to solve this problem because the pattern was predictable.

5. Explain

Students should be able to explain the process they went through to find their answers. Students must be able to talk or write about their thinking. Demonstrate how to write a paragraph describing the steps they took and the decisions they made throughout.

I started with the first layer. I used blocks to make the pyramid and made a list of the number of blocks I used. Then I created a table to record the number of balls in each layer. I made four layers, then saw a pattern. I saw that or each layer, the number of balls used was the number of the layer multiplied by itself. I finished the pattern without the blocks, by multiplying the number of balls that would be in layers 5 and 6. Then I added up each layer. 1 + 4 + 9 + 16 + 25 +36 = 91. I got a total of 91 basketballs

How can you stretch this pattern problem solving strategy?

Find the pattern math problem solving. pattern problem solving.

Math problems can be simple, with few criteria needed to solve them, or they can be multidimensional, requiring charts or tables to organize students' thinking and to record patterns.

In using patterns, it is important for students to find out if the pattern will continue predictably. Have students determine if there is a reason for the pattern to continue, and be sure students use logic when finding patterns to solve problems.

For example, if it rains on Sunday, snows on Monday, rains on Tuesday, and snows on Wednesday, will it rain on Thursday?
Another example: If Lauren won the first and third game of chess, and Walter won the second and fourth game, who will win the fifth game?
Another example: If a plant grew 13 centimeters in the first week and 10 centimeters in the second week, how many centimeters will it grow in the third week?

Because these are questions of probability or nature, be sure students understand why patterns can't be used to find these answers.

The full page is available ONLY to subscribers. Sign up today to get access to this page and all of the content on TeacherVision®.

Featured Middle School Resources

CHOICE BOARDS

Geography Activities for Middle School

Help students explore the world and develop their geography knowledge with this packet of geography activities for middl...

Exit Tickets for Middle School Classrooms

Exit tickets are a form of assessment that are often used informally to assess how well students grasped a lesson, what ...

Test Prep Strategies and Practice for Students

Test Prep Strategies, Tools, and Practice Questions

Help set your students up for academic success with this packet of test-taking tips, test preparation strategies, and pr...

Related Resources

Math problem solving: the guess and check method.

Math Problem Solving: The Guess and Check Method In this article, we will explore the guess and check method, a power...

TEACHING RESOURCE

Problem Solving: Draw a Picture

Problem Solving: Draw a Picture What Is It? The draw a picture strategy is a problem-solving technique in which students...

Problem Solving: Choose the Operation

Problem Solving: Choose the Operation What Is It? The process of "choosing the operation" involves deciding which mathem...

Problem Solving: Make a Table Math Strategy

Math Problem Solving: Make a Table In this introductory guide, we will explore the Make a Table math strategy, a valu...

Problem Solving: Eliminating Possibilities

Problem Solving: Eliminating Possibilities What Is It? Eliminating Possibilities is a strategy in which students remove ...

Problem Solving: Simplify the Problem

Problem Solving: Simplify the Problem What Is It? Simplifying a mathematics problem is a strategy that often is used alo...

Pre-Algebra

Math Review of Equivalent Sentences

More problem-solving strategies: identify subgoals.

Create problem solving journals Students record written responses to open-ended items such as those tested on FCAT in mathematics. Student identifies problem solving strategies.

Authorization for reproduction of this document is hereby granted to persons acting in an official capacity within the State System of Public Education as defined in Section 228.041(1), Florida Statutes. The copyright notice at the bottom of this page must be included in all copies.

The Administrator Assessment and Evaluation Services Florida Department of Education Turlington Building, Room 414 325 West Gaines Street Tallahassee, Florida 32399-0400

My Learning Springboard

School Planning | Academic Tutoring | Test Preparation

A Multidisciplinary Educational Consulting Firm

More results...

Problem-Solving Strategies

January 26, 2021 Brad Hoffman Leave a Comment

$Math-Manipulatives$

Certainly, many students find that it is possible to solve a given word problem with minimal consideration of how to approach it. People have varying degrees of “math sense.” Some find most math problems mysterious. Some, however, can very easily see what to do to find solutions; it almost seems obvious to them. But even for students with strong “math sense,” there come those situations when they don’t intuitively know what to do. For all learners, the recognition of specific problem-solving strategies to solve math problems is useful. Thinking about our own thinking (aka metacognition) is important in developing flexibility so that we can see more than one way to solve a particular problem. Math journaling supports this thinking and development.

Below you will find a list of some very useful problem-solving strategies . One thing that is particularly beneficial about this set of strategies is that they are, in fact, universal. In other words, they will work regardless of the math program a student might be using. Whether it’s Singapore Math or Everyday Math or something else entirely , these problem-solving strategies can provide a clear path toward solutions. Interestingly, they can even extend to problem-solving outside the area of math! Becoming familiar with them and comfortable using them can be a big help to students as they wend their way through problems, be they less or more complex.

10 Problem-Solving Strategies

Make a model/Act out
Draw a diagram or picture
Look for a pattern
Make an organized list
Make a table
Guess & Check
Make it simpler
Work backwards
Use logical reasoning

Here are some examples of problems and how to use these strategies.

“How many complete turns does the hour hand on a clock make in one day?”

From the list of problem-solving strategies above, “make a model or act it out” is an excellent choice for this problem. A student could use a model or a real analog clock and turn the hands and count. Distinguishing between the minute and the hour hand and recognizing that the clock only shows 12 of the 24 hours in a day lets the student see that the hour hand makes two complete turns. A physical clock that a student can actually turn provides an important concrete experience that may prove helpful for finding the solution.

“Using each of the digits 0, 1, 2, 3, 4 only once, make a two-digit number times a three-digit number multiplication problem with the greatest product.”

Students can “ draw a diagram or picture” of an “empty” multiplication problem with a box for each digit. Consider which two digits give the largest product and put them in the highest place value spots. Then, if it’s not immediately evident to the student, use one of the other problem-solving strategies — “ guess and check” — to place the remaining digits in the remaining spots. Check by multiplying the results to identify which is actually the largest (e.g. Is it 430 x 21 or 320 x 41?)

“How many even numbers are there between 201 and 351?”

In this instance, “ look for a pattern” would be especially helpful from the list of problem-solving strategies. Either write all numbers from 201 through 351 and notice the pattern that there are 5 in every set of 10 numbers (e.g. 201-210), and then count how many sets of 10 numbers there are and multiply that by 5, or simply write one set of 10 numbers and identify the 5 in 10 pattern without writing out all of them. Either way is valid.

“You have two noses and three hats. How many different nose-hat disguises can you wear?”

For this problem, “ make an organized list ” from the problem-solving strategies listed above works well. The list will start with Hat A and match with each nose (2), then Hat B with each nose (2), then Hat C with each nose (2). This gives a total of 6 disguises.

“How many numbers between 10 and 30 give a remainder of 2 when divided by 3?” You could “ make a table” to find the solution.

As the Table continues, a pattern becomes evident (“ look for a pattern ” — overlapping strategy!) in which every third number gives a remainder of 2. Count them for a solution.

“If 25 Glinks equal a Glonk, and 15 Glonks equal a Glooie, how many Glinks equal 2 Glooies?”

Please, “ make it simpler”! That strategy is an especially good choice from the list of problem solving-strategies. Let’s look at a simpler, but similar, problem. It’s simpler because the numbers are smaller, and you could even draw a picture to prove it’s correct.

If 3 Glinks equal a Glonk. And 2 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 3×2, which equals 6.

So, if 6 Glinks equal a Glooie, then how many Glinks equal 2 Glooies? Multiply 6×2, which equals 12. So, 12 Glinks equal 2 Glooies.

Now with the larger numbers:

If 25 Glinks equal a Glonk. And 15 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 15×25, which equals 750. So, 750 Glinks equal a Glooie.

Then, how many Glinks equal 2 Glooies? Multiply 750×2, which equals 1500. So, there are 1500 Glinks in 2 Glooies.

It’s the same process, with bigger numbers! Much simpler!

“If I add 10 to my age and double it, I am 90. How old am I?”

From the list of problem-solving strategies, this problem begs for the student to “ work backwards”. Simply un-double the 90 and subtract ten. 90 divided by 2 = 45 and 45-10=35. Voilà! The answer is 35 years old! Then reverse again to confirm that the answer is correct.

“Arrange these digits and symbols to make a true number sentence (equation.) 3,1,4,9,+,/,= (Note: the forward slash [/] signifies “divided by”.)

“ Use logical reasoning ” to realize that any order is possible, but a larger number needs to be divided by a smaller number with no remainder (9/3=3) Then 3+1=4, so the sentence 9/3+1=4 is the solution.

For the problems that seem absolutely impossible to solve, your best option is to “ brainstorm” , and that’s on the above list of problem-solving strategies! Try various ideas; work with a partner; explore to see what might work; try everything you can think of! It’s amazing how good ideas will sometimes just pop into one’s head!

As a student works with these problem-solving strategies, it becomes clear that they often overlap (as in the “ draw a picture” / “guess and check” example above, problem #2). Or a student becomes especially attached to a few particular strategies that often work well. Some problems seem to be especially suitable for a particular strategy, while others can be approached from several directions. Having the flexibility to move from one strategy to another helps avoid the serious “I’m STUCK!” situation. Also, using more than one strategy on the same problem allows students to check solutions more efficiently before moving on. Again, however, THINKING about how we are THINKING is very beneficial in developing skills in this area. We call this metacognition .

Solving word problems can be fun, like being a detective who has unusual insight. There are solutions! Enjoy finding them! And make effective use of problem-solving strategies!

By Jean Snyder and Brad Hoffman , Elementary Math Specialists

$Problem-Solving Strategies$

Company Overview

School Planning

Private Tutoring

Test Preparation

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

What do you know?
What do you need to know?
Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

Identify - What is the question?
Plan - What strategy will I use to solve the problem?
Solve - Carry out your plan.
Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square. 18 + 2 = 20 If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square 61 + (3 x 7) = 82 If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

My presentations

Auth with social network:

Download presentation

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

Presentation is loading. Please wait.

To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video

Problem-Solving Strategy: Look for a pattern

Published by Theodore Wells Modified over 9 years ago

Presentation on theme: "Problem-Solving Strategy: Look for a pattern"— Presentation transcript:

4.7: Arithmetic sequences

Digital/ Analog Time 4th Strategies for Your Toolbox in Solving Problems Involving Digital/ Analog Time.

First Grade Newsletter February 10, 2012 Important Dates and Events Feb. 17 th Valentine’s Day Party Please have your child make their Valentine’s Day.

Warm Up Find the next two numbers in the pattern, using the simplest rule you can find. 1. 1, 5, 9, 13, , 50, 25, 12.5, , 87, 94,

Arithmetic Sequences Explicit Formula.

Do Now “Alien Activity” on my website….find the ordered pair where each space invader is located.

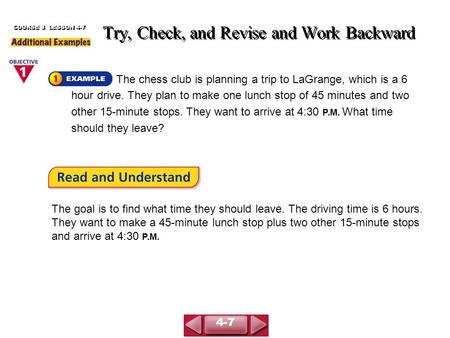
The chess club is planning a trip to LaGrange, which is a 6 hour drive. They plan to make one lunch stop of 45 minutes and two other 15-minute stops. They.

Warm Up 1. 3x 2 + 2x –x 4 + 3x 3 – 3x Add or subtract the following polynomials Solve.

Module 2 Topic A Lesson 3 Metric Unit Conversions

{ Adding Fractions November 3, I will add fractions with unlike units using the strategy of creating equivalent fractions GOAL:

7.8 Work Problems Purpose: To solve word problems involving to job rates working together to get one job done. Homework: Finish Worksheet and p

WARM UP 1. A number that is part of 100 is the ______________ of the number is what percent of 80? 3. 20% of 40 is what number? 4. 7 is 5% of what.

2.4 Use the Binomial Theorem Test: Friday.

Pre-Algebra HOMEWORK Page 606 #1-9.

1-5 Mental Math Warm Up Problem of the Day Lesson Presentation

Inductive and Deductive Reasoning. Inductive Observing the data, recognizing a pattern and making generalizations Do you see a pattern Can you describe.

Classic Math Problems with Numbers Today’s Learning Goal We will learn how to read algebra word problems to help us solve them. We will apply the steps.

Splash Screen. Lesson Menu Five-Minute Check (over Lesson 9–5) Main Idea Example 1:Problem-Solving Strategy.

Monday, October 27th Math Homework Multiplication worksheet & study multiplication facts Students: HW ready to check.

About project

PRINT TO PLAY
DIGITAL GAMES

Problem-Solving Strategies

October 16, 2019

There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.

Problem-solving strategies

1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.

Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.

Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?

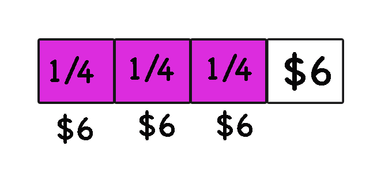
2. Guess and check

Teach students the same strategy research mathematicians use.

With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly. By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.

Find two numbers that have sum 11 and product 24.

Try/guess 5 and 6 the product is 30 too high

adjust to 4 and 7 with product 28 still high

adjust again 3 and 8 product 24

3. Make a table or a list

Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.

To make sure you are listing all the information correctly read the problem carefully.

Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.

Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?

A table or list is useful in solving logic problems.

Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.

Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.

Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.

5. Find a pattern.

Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.

The “rule” can then be used to find the answer to the question and complete the table/list.

Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?

6. Working backward

Problems that can be solved with this strategy are the ones that list a series of events or a sequence of steps .

In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.

Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.

For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.

The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.

8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took

8+31+5+4= 48 Answer: The box came with 48 pieces of candy.

Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.

Print and digital activities

I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.

sample below

How to use the activity cards

Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.

Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.

For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.

Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.

Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions

There are 2 versions of the resource

70 google slides with explanations + 70 printable task cards

70 google slides with explanations + 11 worksheets

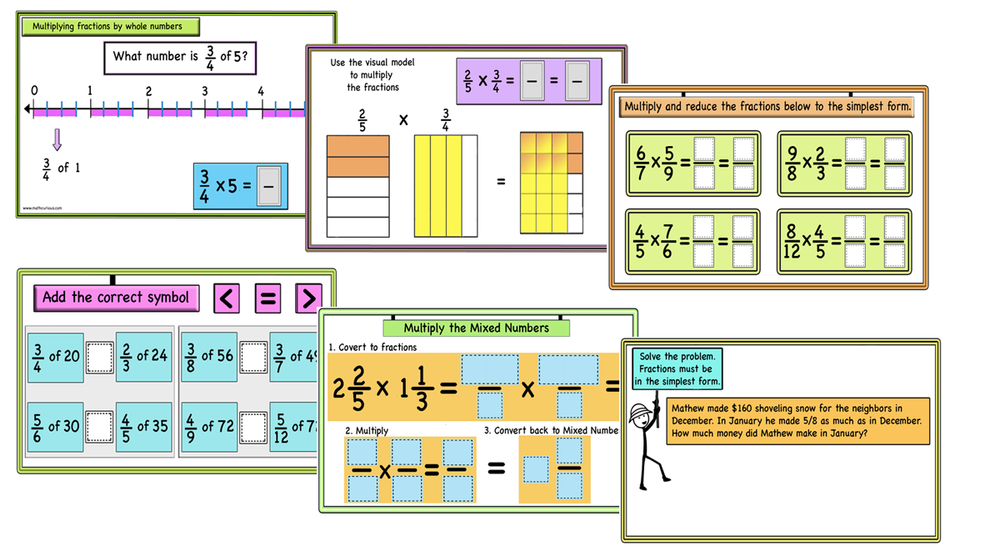
Multiplying fractions/mixed numbers/simplifying

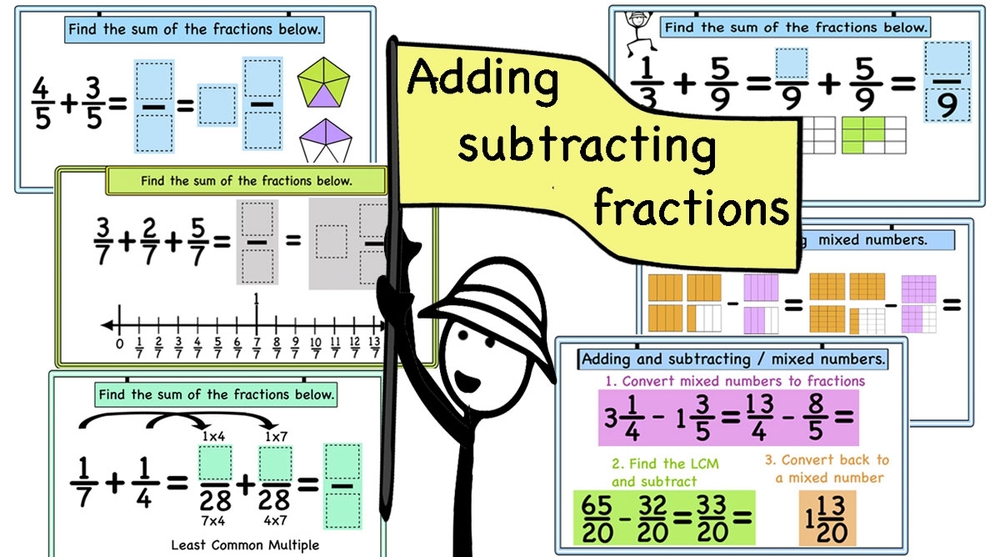
Adding and subtracting fractions

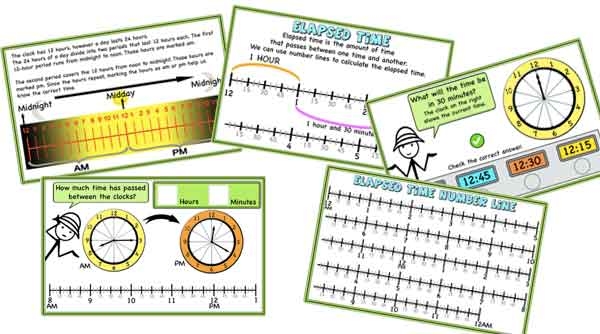
AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities

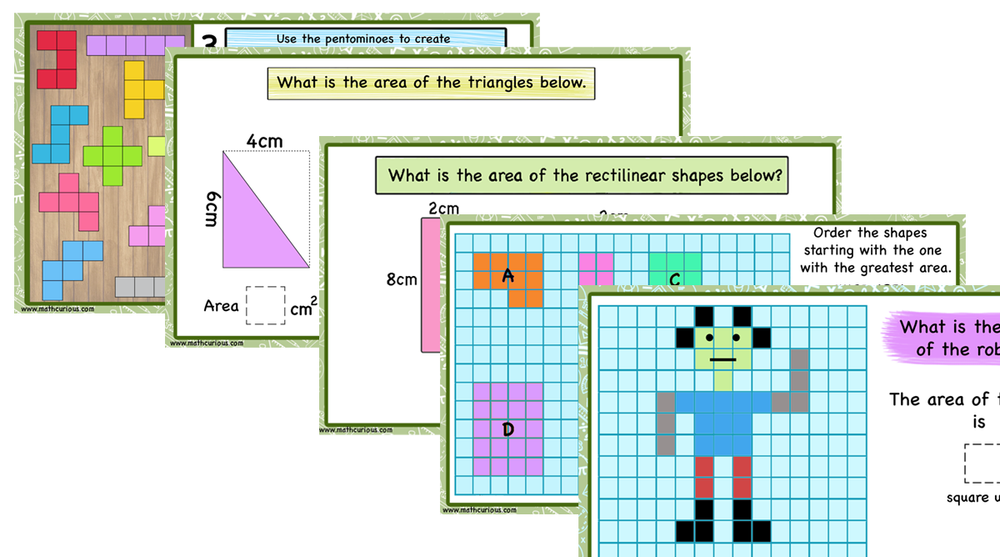
Teaching area, ideas, games, print, and digital activities

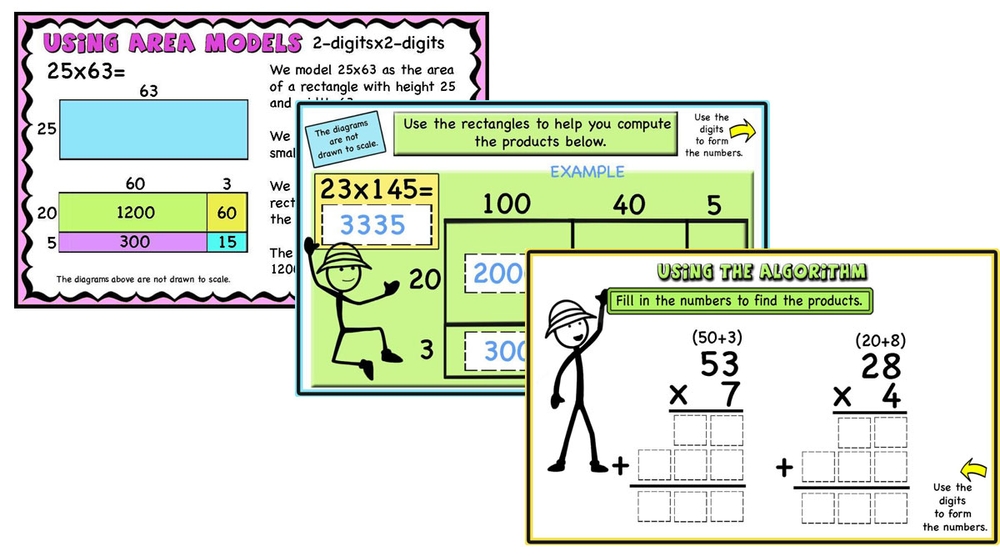
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems

Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division

Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike

Diving into Division -Teaching division conceptually

Expressions with arrays

Decimals, Decimal fractions, Percentages – print and digital

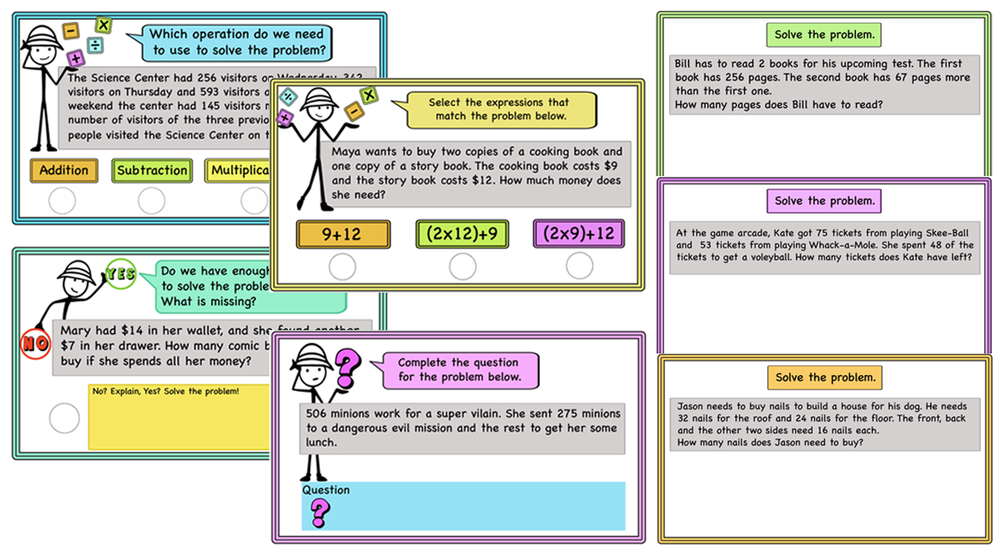
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital

Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape

A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game

Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…

Problem-Solving Strategy: Look for a pattern

Mar 23, 2019

240 likes | 573 Views

Problem-Solving Strategy: Look for a pattern. Objective: Solve problems by looking for a pattern. 2-6 Problem-Solving Strategy: Look for a Pattern. Example

Share Presentation

problems worked
fibonacci numbers
sara worked 30 min

Presentation Transcript

Problem-Solving Strategy: Look for a pattern Objective: Solve problems by looking for a pattern.

2-6 Problem-Solving Strategy: Look for a Pattern Example Sara was trying to finish all her math homework on Friday. She did 3 problems the first 30 minutes, 4 problems the next 30 minutes, 6 problems the next 30 minutes, 9 problems the next 30 minutes, and so forth. If she continues to work at this rate, how many problems will she have done in 4 hours. Explore Sara worked 30 min per problem set. Time worked number of problems worked 1st 30 min 3 2nd 30 min 4 3rd 30 min 6 4th 30 min 9

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 Time worked: 1hr

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 6 9 Time worked: 1hr 2hr

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 6 9 13 18 Time worked: 1hr 2hr 3hr

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 6 9 13 18 24 31 Time worked: 1hr 2hr 3hr 4hr

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 6 9 13 18 24 31 Time worked: 1hr 2hr 3hr 4hr 3 + 4 + 6 + 9 + 13 + 18 + 24 + 31 =

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 6 9 13 18 24 31 Time worked: 1hr 2hr 3hr 4hr 3 + 4 + 6 + 9 + 13 + 18 + 24 + 31 = 108 problems

2-6 Problem-Solving Strategy: Look for a Pattern Solve Problems worked: 3 4 6 9 13 18 24 31 Time worked: 1hr 2hr 3hr 4hr 3 + 4 + 6 + 9 + 13 + 18 + 24 + 31 = 108 problems Examine Do the number of problems worked each half hour follow the pattern?

2-6 Problem-Solving Strategy: Look for a Pattern Write a rule to find the successive terms in the pattern. 63, 48, 35, 24, . . . . . .

2-6 Problem-Solving Strategy: Look for a Pattern Write a rule to find the successive terms in the pattern. 63, 48, 35, 24, . . . . . . The number decreased by 15, then 13, then 11, so the next number should decrease by 9 and then by 7. The number subtracted decreases by two each time.

2-6 Problem-Solving Strategy: Look for a Pattern The pattern of numbers, 1, 1, 2, 3, 5, 8, . . . . ., is called the Fibonacci sequence. The terms of the sequence are called the Fibonacci numbers. List the first ten Fibonacci numbers.

2-6 Problem-Solving Strategy: Look for a Pattern Find a pattern for the following numbers. 1, 3, 5, 8, 11, 15, 19, . . . . . .

2-6 Problem-Solving Strategy: Look for a Pattern Find a pattern for the following numbers. 1, 3, 5, 8, 11, 15, 19, . . . . . . Pattern: +2, +2, +3, +3, +4, +4, +5, +5, . . .

2-6 Problem-Solving Strategy: Look for a Pattern Find the number that should be in the blank space. 1, 24, 2, 23, 3, 22, 4, . . . . . . 12, 13, 13, __ 12

2-6 Problem-Solving Strategy: Look for a Pattern Find the number that should be in the blank spaces. 1, 4, 10, 20, 35, 56, __, __, __

2-6 Problem-Solving Strategy: Look for a Pattern Find the number that should be in the blank spaces. 1, 4, 10, 20, 35, 56, __, __, __ 84, 120

More by User

Basics Menu

Basics Menu Learning Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . page 2 Problem Solving Steps in the Problem Solving Process . . . . . . . . . . . . . . . . . . page 3

1.17k views • 85 slides

Pattern-Directed Inference Systems

Pattern-Directed Inference Systems. Algorithms and Data Structures II Academic Year 2002-03. Previous Lectures. (Classical) Problem Solving Separation of problem space and search engine Characterization of problem space Pluggable search engines

1.35k views • 93 slides

Classical Problem Solving

Classical Problem Solving. Design of Computer Problem Solvers CS 344 Winter 2000. Last time. AI programming versus conventional programming Emphasis on knowledge representation Overview of systems Homework 0 Preview of homework 1. This week’s themes.

1.3k views • 87 slides

Problem-Solving Items in PSLE Mathematics

Problem-Solving Items in PSLE Mathematics. Yeap Ban Har National Institute of Education Nanyang Technological University. Organised by Association of Mathematics Educators & Department of Science and Mathematics Singapore Polytechnic. Singapore Mathematics Curriculum (1992, 2001).

1.6k views • 61 slides

Implementing the Problem-Solving/Response to Intervention

Implementing the Problem-Solving/Response to Intervention. Minooka School District 201 Response to Intervention. If we can really understand the problem, the answer will come out of it, because the answer is not separate from the problem. -Krishnamurti.

1.05k views • 87 slides

CHAPTER 2 PROBLEM SOLVING

CHAPTER 2 PROBLEM SOLVING . This chapter will cover the following topics: Problem Solving Concepts for the Computer Pre-Programming Phase Programming Or Implementation Phase. What Problem Can Be Solved By Computer.

2.13k views • 109 slides

Theory of Inventive Problem-Solving

TRIZ . Theory of Inventive Problem-Solving. Damian Gordon. Introduction. T heoria R esheneyva I sobretatelskehuh Z adach ( Theory of Solving Problems Inventively). Introduction. Developed by Soviet engineer Genrich Altshuller and his colleagues, beginning in 1946.

1.99k views • 110 slides

Problem Solving

Problem Solving. Applied Thinking. Three Forms of Applied Thinking. According to John Adair in “Decision Making & Problem Solving Strategies” there are three forms of applied thinking needed:. Applied Thinking. Why we need to use Applied Thinking. Understanding how the Mind works.

320 views • 0 slides

Splash Screen

Splash Screen. Lesson 1-1 A Plan for Problem Solving Lesson 1-2 Powers and Exponents Lesson 1-3 Squares and Square Roots Lesson 1-4 Order of Operations Lesson 1-5 Problem-Solving Investigation: Guess and Check Lesson 1-6 Algebra: Variables and Expressions Lesson 1-7 Algebra: Equations

2.48k views • 201 slides

Team-Initiated Problem Solving (TIPS) Brief Overview

Team-Initiated Problem Solving (TIPS) Brief Overview. Presented by: November 2013 Acknowledgements to: Rob Horner & Steve Newton, University of Oregon & Bob Algozzine , Kate Algozzine & Dale Cusumano at University of North Carolina at Charlotte www.uoecs.org. Anne W. Todd

1.15k views • 97 slides

The Collaborative Problem Solving Approach: Making it work for kids on the spectrum

Diane Durante MEPD, OTR, CST I Presentation modified from and based on the work of Stuart Ablon , Ph.D . & Ross Greene, Ph.D. for the Central Wisconsin Autism Society November 4, 2010. The Collaborative Problem Solving Approach: Making it work for kids on the spectrum.

2.06k views • 93 slides

Psychology of Problem Solving

Psychology of Problem Solving. Arash Rastegar Department of Mathematical Sciences Sharif University of Technology. There are two kinds of Mathematicians. Problem Solvers Contribute Local to global point of view Interesting special cases. Theoriticians Contribute

1.63k views • 120 slides

TIPS: Team Initiated Problem Solving

TIPS: Team Initiated Problem Solving. Review Status and Identify Problems. Collect and Use Data. Evaluate and Revise Action Plan. Develop and Refine Hypotheses. Anne Todd, University of Oregon Celeste Rossetto Dickey, University of Oregon. Discuss and Select Solutions.

1.19k views • 90 slides

PROBLEM SOLVING AND DECISION MAKING

PROBLEM SOLVING AND DECISION MAKING. ICE BREAKER. ICEBREAKER. What is your leisure activity? Who , living or dead , do you most admire , and why? What is your greatest achievement? What are your positive qualities?

2.5k views • 139 slides

Collaborative Problem Solving

Collaborative Problem Solving. Presented by. YOUR NAME HERE!. Course overheads. Recent Notes on Community Policing. 1974: Kansas City Preventive Patrol 1980: Rapid Response Studies 1981: Differential Response Studies Foot Patrols Broken Windows/Fear Reduction

1.72k views • 142 slides

PROBLEM SOLVING & DECISION MAKING

PROBLEM SOLVING & DECISION MAKING. Learning Objectives. At the end of the training, participants are expected to : Understand how to use an innovative yet structured process-based problem solving approach in practical scenarios. Recognize how to take informed decisions and calculated risks.

5.71k views • 84 slides

Critical Thinking & Problem Solving Strategies

Critical Thinking & Problem Solving Strategies. Debbie Dillman, MSRS, RT(R) Program Chair, Radiologic Technology Ivy Tech Community College, Marion, IN. Objectives. Define critical thinking Discuss the major elements of critical thinking Name the components of critical thinking

6.95k views • 78 slides

Creativity and Creative Problem Solving

Creativity and Creative Problem Solving. Minder Chen Professor of MIS California State University Channel Islands [email protected]. Creativity and Innovation.

1.62k views • 90 slides

8 Discipline Methodology (Team Oriented Problem Solving) The SunPower Way

8 Discipline Methodology (Team Oriented Problem Solving) The SunPower Way. An essential part of Continual Improvement and Problem Prevention. June 2008. Audience. Audience: This class is designed for individuals seeking a basic understanding of the SunPower 8-D Problem Solving Methodology.

2.18k views • 128 slides

Introduction to Process Problem Solving

Introduction to Process Problem Solving. - Section 1 -. Introductions. Facilitator Participants Safety. Define and resolve problems using Process Problem Solving: Standards Root cause analysis Problem red flags Corrective actions. Defining a Problem. Problems:

1.37k views • 81 slides

CULTURAL SWARMS: KNOWLEDGE-DRIVEN PROBLEM SOLVING IN SOCIAL SYSTEMS

CULTURAL SWARMS: KNOWLEDGE-DRIVEN PROBLEM SOLVING IN SOCIAL SYSTEMS. Robert G. Reynolds. Department of Computer Science, Wayne State University Museum of Anthropology, University of Michigan. The Emergence of Social Intelligence and Socially Motivated Problem Solving.

1.02k views • 86 slides

Strong Method Problem Solving

7. Strong Method Problem Solving. 7.0 Introduction 7.1 Overview of Expert System Technology 7.2 Rule-Based Expert Systems 7.3 Model-Based, Case Based, and Hybrid Systems. 7.4 Planning 7.5 Epilogue and References 7.6 Exercises. Chapter Objectives.

1.67k views • 105 slides

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Problem Solving by Finding a Pattern

Finding Patterns in Math Problems:

And of course, don’t miss the other posts in this Math Problem Solving Series:

One Comment

Similar Posts

Valentine’s Day STEM: Build a Tower with Conversation Hearts

8 Reasons Making Mistakes in Math is a GOOD Thing!

Weekly Math Freebie Round Up!

Teach Kids to Be Curious Like Einstein

September Problem of the Day Calendar

Add & Subtract Decimals on a Number Line {FREE Printable Number Lines!}

Math Time Doesn't Have to End in Tears

Pattern Problem Solving: Teach Students to Find a Pattern in Math Problems

Pattern problem solving

What is pattern problem solving?

Why is pattern problem solving important?

How to teach students to find the pattern in a math problem (using an example)

1. Ensure students understand the problem

2. Choose a pattern problem solving strategy

3. Solve the problem

4. Check your students' answers

5. Explain

How can you stretch this pattern problem solving strategy?

Featured Middle School Resources

Geography Activities for Middle School

Exit Tickets for Middle School Classrooms

Test Prep Strategies, Tools, and Practice Questions

Related Resources

Problem Solving: Draw a Picture

Problem Solving: Choose the Operation

Problem Solving: Make a Table Math Strategy

Problem Solving: Eliminating Possibilities

Problem Solving: Simplify the Problem

More Problem-Solving Strategies: Look for a Pattern

Math Review of Equivalent Sentences

Problem-Solving Strategies

10 Problem-Solving Strategies

Leave a Reply Cancel reply

Company Overview

School Planning

Private Tutoring

Test Preparation

Math Problem Solving Strategies

Problem Solving Strategies

Solving Word Problems

Problem Solving Strategy: Guess And Check

Problem Solving : Make A Table And Look For A Pattern

Find A Pattern Model (Intermediate)

The following are some other examples of problem solving strategies.

Auth with social network:

Presentation on theme: "Problem-Solving Strategy: Look for a pattern"— Presentation transcript:

About project

Problem-Solving Strategies

Problem-solving strategies

2. Guess and check

3. Make a table or a list

5. Find a pattern.

6. Working backward

Print and digital activities

You might also like

Multiplying fractions/mixed numbers/simplifying

Adding and subtracting fractions

AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities

Teaching area, ideas, games, print, and digital activities

Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems

Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division

Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike

Diving into Division -Teaching division conceptually

Expressions with arrays

Decimals, Decimal fractions, Percentages – print and digital

Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital

Chicken Escape

Dragon Times – A math Adventure card game

Problem-Solving Strategy: Look for a pattern

Share Presentation

Presentation Transcript

Basics Menu

Pattern-Directed Inference Systems

PROBLEM SOLVING & DECISION MAKING

Critical Thinking & Problem Solving Strategies