ib math ia research question

IB Maths IA: 60 Examples and Guidance

Charles Whitehouse

The International Baccalaureate Diploma Programme offers a variety of assessments for students, including Internal Assessments (IAs), which are pieces of coursework marked by students’ teachers. The Mathematics Internal Assessment follows the same assessment criteria across Mathematics Analysis and Approaches (AA) and Mathematics Application and Interpretation (AI). It forms 20% of a student’s Mathematics grade.

The International Baccalaureate (IB) made several changes to the curriculum and assessment methods, particularly in Mathematics. As of 2024, the IB has updated the syllabi for Mathematics Analysis and Approaches (AA) and Mathematics Applications and Interpretation (AI). The IAs now include a greater emphasis on real-world applications and data analysis.

In this article, we will cover everything you need to know about the IB Mathematics IA, including the structure, assessment criteria, and some tips for success.

What is the Mathematics IA?

The Maths IA is an individual exploration of an area of mathematics, based on the student’s own work with guidance from their teacher. Mathematical communication is an important part of the IA, which should be demonstrated through both effective written communication and use of formulae, diagrams, tables, and graphs. A top-rated Singapore IB tutor recommended that the exploration should be 10 to 15 pages long and students will spend 8 to 12 hours on the work.

Even A-Level Maths tutors and A-Level Further Maths tutors have found the concept of an IA-like component in IB Maths to be both challenging and rewarding, enriching the learning experience.

To learn more about the IB Maths Internal Assessment, you can have a look at the IB Maths AA resources as well as the IB Maths AI resources :

• IB Maths AA Past Papers
• IB Maths AI Past Papers

Boost your grades with our revision platform , used by 100,000+ students!

Access thousands of practice questions, study notes, and past papers for every subject.

What are the assessment criteria?

Like most IB IAs, the IB Maths IA is marked on a group of 5 criteria which add up to 20 marks. Online Maths tutors recommend to look through these carefully before and during your investigation, to ensure that you are hitting the criteria to maximise your mark.

Source : IB Mathematics Applications and Interpretation Guide

Criterion A: Communication (4 marks) – This refers to the organisation and coherence of your work, and the clarity of your explanations. The investigation should be coherent, well-organized, and concise.

Criterion B: Mathematical Presentation (4 marks) – This refers to how well you use mathematical language, including notation, symbols and terminology. Your notation should be accurate, sophisticated, and consistent. Define your key terms and present your data in a varied but proper way (including labelling those graphs).

Criterion C: Personal Engagement (3 marks) – There should be evidence of outstanding personal engagement in the IA. This is primarily demonstrated through showing unique thinking, not just repeating analysis found in textbooks. This can be evidenced through analysing independently or creatively, presenting mathematical ideas in their own way, exploring the topic from different perspectives, making and testing predictions.

Criterion D: Reflection (3 marks) – This refers to how you evaluate both your sources and the strengths and weaknesses of any methodology you use. There should be “substantial evidence of critical reflection”. This could be demonstrated by considering what another stage of investigation could be, discussing implications of results, discussing strengths and weaknesses of approaches, and considering different perspectives.

Criterion E: Use of Mathematics (6 marks ) –

Note that only 6 marks are available for the actual use of mathematics! The focus of the investigation is on explaining well and analysing with genuine, personal curiosity. The level of mathematics expected also depends on the level the subject is studied at: Standard Level students’ maths is expected to be “correct”, while Higher Level students’ maths is expected to be “precise” and demonstrate “sophistication and rigour”. Use of Mathematics has been updated to emphasize the importance of not only correctness but also the innovative application of mathematical concepts.

Examiners are primarily looking for thorough understanding, which also requires clear communication of the principles behind the mathematics used - not just coming to the right answer.

Have a look at our comprehensive set resources for IB Maths developed by expert IB teachers and examiners!

- IB Maths AI SL Study Notes

- IB Maths AI HL Study Notes

- IB Maths AA SL Study Notes

- IB Maths AA HL Study Notes

What are some example research questions?

Students should choose a research area that they are interested in and have a comprehensive understanding of. Often, student may choose to consult with an expert IB Maths tutor to help them decide a good question. It should have a link to something of personal interest, as indicated by Criterion C. Popular topics include Calculus, Algebra and Number (proof), Geometry, Statistics, and Probability, or Physics. Some students make links between Math and other subjects – a good way to combine knowledge from your other IB courses!

Here are examples with details of potential research questions that could inspire your Mathematics IA:

1 - Investigating the properties of fractals and their relationship to chaos theory.

Use computer software or mathematical equations to generate and analyze fractals. Explore the patterns and properties of the fractals, such as self-similarity and complexity. Investigate how changes in the initial conditions or parameters affect the resulting fractals. Analyze the relationship between fractals and chaos theory, and how fractals can be used to model chaotic systems. Present findings through visual representations and data analysis.

2 - Analyzing the behavior of recursive sequences and their applications in computer science and cryptography.

Use mathematical formulas to generate recursive sequences and analyze their behavior. This could involve plotting the sequences and observing patterns, finding closed-form expressions for the sequences, and exploring their applications in computer science and cryptography. For example, recursive sequences can be used in algorithms for sorting and searching data, and in encryption methods such as the Fibonacci cipher. The results of the analysis could be presented in a research paper or presentation.

3 - Exploring the properties of different types of differential equations and their applications in physics and engineering.

Conduct research on the different types of differential equations and their applications in physics and engineering. This could involve studying examples of differential equations used in fields such as fluid dynamics, electromagnetism, and quantum mechanics. The properties of each type of differential equation could be analyzed, such as their order, linearity, and homogeneity. The applications of each type of differential equation could also be explored, such as how they are used to model physical systems and solve engineering problems. The findings could be presented in a report or presentation.

4 - Investigating the properties of chaotic dynamical systems and their applications in physics and biology.

Use computer simulations to model chaotic dynamical systems and explore their behavior. This could involve studying the Lorenz attractor, the logistic map, or other well-known examples of chaotic systems. The simulations could be used to investigate the sensitivity of the systems to initial conditions, the presence of strange attractors, and other key features of chaotic dynamics. The results could then be applied to real-world systems in physics and biology, such as weather patterns, population dynamics, or chemical reactions.

5 - Designing an optimized route for a delivery service to minimize travel time and fuel costs.

Use a computer program or algorithm to analyze data on the locations of delivery destinations and the most efficient routes to reach them. The program would need to take into account factors such as traffic patterns, road conditions, and the size and weight of the packages being delivered. The output would be a map or list of optimized delivery routes that minimize travel time and fuel costs. This could be used to improve the efficiency and profitability of the delivery service.

6 - Developing a model to predict the spread of infectious diseases in a population.

Collect data on the population size, infection rate, and transmission rate of the disease in question. Use this data to create a mathematical model that simulates the spread of the disease over time. The model should take into account factors such as population density, age distribution, and vaccination rates. The accuracy of the model can be tested by comparing its predictions to real-world data on the spread of the disease. The model can be used to explore different scenarios, such as the impact of different vaccination strategies or the effectiveness of quarantine measures.

7 - Investigating the relationship between different geometric shapes and their properties.

Conduct a series of experiments in which different geometric shapes are tested for various properties such as volume, surface area, and weight. The data collected could then be analyzed to determine if there is a relationship between the shape of an object and its properties. This could involve creating 3D models of the shapes using computer software, or physically measuring the shapes using laboratory equipment. The results could be presented in a graph or chart to illustrate any trends or patterns that emerge.

8 - Analyzing the behavior of projectile motion and its applications in physics.

Conduct experiments in which a projectile is launched at different angles and velocities, and its trajectory is tracked using high-speed cameras or other measurement devices. The data collected can be used to analyze the motion of the projectile and determine its velocity, acceleration, and other physical properties. This information can then be applied to real-world scenarios, such as designing rockets or calculating the trajectory of a ball in sports. Additionally, the behavior of projectile motion can be studied in different environments, such as in the presence of air resistance or in a vacuum, to better understand its applications in physics.

9 - Developing a model to predict the path of a planet based on gravitational forces.

Collect data on the mass, position, and velocity of the planet at a given time. Use the law of gravitation to calculate the gravitational forces acting on the planet from other celestial bodies in the system. Use this information to predict the path of the planet over time, taking into account any changes in velocity or direction caused by gravitational forces. The accuracy of the model could be tested by comparing its predictions to observations of the planet's actual path.

10 - Investigating the properties of conic sections and their applications in geometry and physics.

Use mathematical equations to explore the properties of conic sections such as circles, ellipses, parabolas, and hyperbolas. Investigate their applications in geometry, such as in the construction of satellite dishes and reflectors, and in physics, such as in the orbits of planets and comets. Develop models and simulations to demonstrate these applications and their impact on real-world scenarios.

Get expert help with IB Maths

The world's leading online IB Maths tutoring provider trusted by students, parents, and schools globally.

4.93 /5 based on 509 reviews

11 - Modeling the spread of a virus through a population and analyzing the effectiveness of different intervention strategies.

Develop a mathematical model that simulates the spread of the virus through a population. The model would need to take into account factors such as the infectiousness of the virus, the rate of transmission between individuals, and the effectiveness of different intervention strategies such as social distancing or vaccination. The model could then be used to analyze the effectiveness of different intervention strategies and predict the potential impact of future outbreaks. The output of the model would be a set of data and visualizations that show the predicted spread of the virus and the effectiveness of different intervention strategies.

12 - Modeling the spread of a rumor or disease through a network and analyzing the impact of network topology.

Develop a mathematical model that simulates the spread of the rumor or disease through a network. The model should take into account factors such as the probability of transmission between individuals, the rate of recovery or decay of the rumor or disease, and the structure of the network. The impact of network topology could be analyzed by comparing the spread of the rumor or disease in different types of networks, such as random, scale-free, or small-world networks. The results of the simulation could be visualized using graphs or heat maps to show the spread of the rumor or disease over time.

13 - Developing a model to predict the growth of a population over time.

Collect data on the current population size and growth rate of the population over a period of time. Use this data to develop a mathematical model that predicts the population growth rate over time. The model could be tested by comparing its predictions to actual population growth data from previous years. The model could also be used to predict future population growth and to identify factors that may affect the population's growth rate.

14 - Investigating the properties of exponential functions and their applications in finance and economics.

Develop a mathematical model for an exponential function, including its domain and range, growth/decay rate, and asymptotes. Use this model to analyze real-world scenarios in finance and economics, such as compound interest, population growth, or stock market trends. Graph the function and interpret the results in terms of the original problem.

15 - Developing a model to predict the outcomes of a sporting event based on historical data and team statistics.

Collect historical data on the two teams playing in the sporting event, including their win-loss records, player statistics, and any relevant trends or patterns. Use this data to develop a statistical model that predicts the outcome of the game based on these factors. The model can then be tested and refined using additional data and feedback from experts in the field. The final output would be a prediction of the outcome of the game, along with a measure of the model's accuracy and any potential limitations or uncertainties.

16 - Analyzing the behavior of different types of sequences and their convergence or divergence.

Use mathematical models and computer simulations to analyze the behavior of different types of sequences. This would involve testing various sequences for convergence or divergence, and comparing their behavior under different conditions. The results of these simulations could be used to develop new mathematical theories and algorithms for analyzing sequences, and could have applications in fields such as computer science, physics, and engineering.

17 -Investigating the properties of different types of angles and their relationship to geometry and trigonometry.

Conduct a study of different types of angles, including acute, obtuse, right, and straight angles. Explore their properties, such as their degree measurements, relationships to other angles, and their use in geometry and trigonometry. This could involve creating visual aids, such as diagrams or graphs, to illustrate the concepts being studied. The results of the study could be presented in a report or presentation format, highlighting the key findings and insights gained from the investigation.

18 - Developing a model to predict the outcomes of a game based on probability theory.

Collect data on the outcomes of previous games, including the teams playing, the score, and any relevant factors such as weather conditions or injuries. Use this data to calculate the probability of each team winning based on various factors. Develop a model that takes into account these probabilities and predicts the outcome of future games. The model would need to be tested and refined using additional data and statistical analysis. The final output would be a reliable model for predicting the outcomes of games based on probability theory.

19 - Analyzing the behavior of different types of inequalities and their applications in algebra and calculus.

Create a graph to visually represent the behavior of different types of inequalities, such as linear, quadratic, and exponential inequalities. Use examples to demonstrate how these inequalities can be applied in algebra and calculus, such as finding the maximum or minimum value of a function subject to certain constraints. Additionally, provide real-world applications of these concepts, such as optimizing production processes or predicting population growth.

20 - Investigating the properties of different types of graphs and their applications in computer science and social science.

Conduct a literature review to identify the different types of graphs and their applications in computer science and social science. Develop a set of criteria for evaluating the effectiveness of different types of graphs in conveying information and insights. Use these criteria to analyze and compare several examples of graphs from each field. Based on the analysis, identify the most effective types of graphs for different types of data and research questions in each field. Develop guidelines for selecting and creating effective graphs in computer science and social science research.

21 - Analyzing the behavior of different types of matrices and their applications in linear algebra and quantum mechanics.

Conduct experiments to test the behavior of different types of matrices in linear algebra and quantum mechanics. For example, in linear algebra, the inverse of a matrix can be calculated and used to solve systems of linear equations. In quantum mechanics, matrices are used to represent quantum states and operators. The behavior of these matrices can be analyzed by performing matrix operations and observing the resulting changes in the system. The applications of these matrices in various fields can also be explored and analyzed.

22 - Developing a model to predict the outcomes of a business investment based on market trends and financial data.

Collect and analyze market trends and financial data relevant to the business investment. This could include factors such as industry growth rates, consumer demand, and financial statements of similar companies. Using this data, develop a predictive model that takes into account various variables and their potential impact on the investment. The model could be tested and refined using historical data and adjusted as new information becomes available. The output would be a prediction of the potential outcomes of the investment based on the model's calculations.

23 - Modeling the spread of a forest fire and analyzing the effectiveness of different containment strategies.

Develop a computer model of the forest fire spread using data on wind direction, temperature, humidity, and fuel load. The model could be calibrated using historical data on past forest fires to ensure its accuracy. Different containment strategies could then be simulated in the model, such as creating fire breaks or using water or fire retardant chemicals to slow the spread of the fire. The effectiveness of each strategy could be evaluated by comparing the simulated fire spread with and without the strategy in place.

24 - Analyzing the behavior of different types of optimization problems and their applications in engineering and computer science.

Conduct a literature review to identify different types of optimization problems and their applications in engineering and computer science. Develop a framework for analyzing the behavior of these problems, taking into account factors such as the size of the problem, the complexity of the solution space, and the type of optimization algorithm used. Apply this framework to a set of case studies, comparing the performance of different optimization algorithms and identifying best practices for solving different types of optimization problems.

25 - Investigating the properties of different types of geometric transformations and their applications in computer graphics and animation.

Conduct a literature review to gather information on the properties of different geometric transformations and their applications in computer graphics and animation. This could include translations, rotations, scaling, and shearing. Develop a set of test cases to demonstrate the use of these transformations in creating different types of graphics and animations. The results of these tests could be used to compare the effectiveness of different types of transformations for different applications. Additionally, the limitations and challenges associated with each transformation could be identified and discussed.

26 - Developing a model to predict the outcomes of an election based on polling data.

Collect polling data from a representative sample of the population and analyze it using statistical methods such as regression analysis or machine learning algorithms. The model would need to be trained on historical election data to ensure its accuracy. The output of the model would be a prediction of the likely outcome of the election based on the polling data and the historical trends. The model could also be used to identify key factors that are driving voter behavior and to test different scenarios, such as changes in voter turnout or shifts in public opinion.

27 - Analyzing the behavior of different types of integrals and their applications in calculus and physics.

Conduct a series of experiments to analyze the behavior of different types of integrals, such as definite and indefinite integrals, and their applications in calculus and physics. For example, one experiment could involve calculating the area under a curve using both definite and indefinite integrals and comparing the results. Another experiment could involve analyzing the motion of an object using calculus and determining its velocity and acceleration at different points in time. The results of these experiments could be used to develop a deeper understanding of the behavior of integrals and their applications in various fields.

28 - Studying the properties of different types of probability distributions and their applications in statistics and finance.

Conduct a literature review to gather information on different types of probability distributions and their applications in statistics and finance. Develop a theoretical framework to analyze the properties of these distributions and their relevance in different contexts. Use statistical software to simulate data and test the theoretical framework. Analyze the results and draw conclusions about the usefulness of different probability distributions in various applications.

29 - Developing a model to predict the outcomes of a marketing campaign based on consumer data.

Collect consumer data such as demographics, purchasing habits, and social media activity. Use this data to identify patterns and trends that can be used to develop a predictive model. The model would need to be trained using historical data on marketing campaigns and their outcomes. Once the model is trained, it can be used to predict the outcomes of future marketing campaigns based on the input data. The accuracy of the model can be tested by comparing its predictions to the actual outcomes of the campaigns.

30 - Investigating the properties of different types of symmetry and their relationship to geometry and physics.

Conduct a study of different types of symmetry, such as bilateral, radial, and rotational symmetry. This could involve creating models or diagrams of different symmetrical shapes and analyzing their properties, such as the number of axes of symmetry and the angles of rotation. The relationship between symmetry and geometry could be explored by examining how different symmetrical shapes can be used to create geometric patterns. The relationship between symmetry and physics could be investigated by exploring how symmetrical structures are used in physics, such as in the design of crystals or the study of particle physics.

31 - Modeling the spread of a rumor or news story through a population and analyzing its impact.

Develop a mathematical model that simulates the spread of the rumor or news story through a population. This model could take into account factors such as the initial number of people who hear the rumor, the rate at which they share it with others, and the likelihood that each person will believe and share the rumor. The impact of the rumor could be analyzed by looking at factors such as changes in people's behavior or attitudes, or the spread of related rumors or misinformation. The model could be refined and tested using data from real-world examples of rumor or news story propagation.

32 - Analyzing the behavior of different types of exponential growth and decay functions and their applications in science and engineering.

Use mathematical models to analyze the behavior of exponential growth and decay functions. This could involve studying the equations that describe these functions, graphing them to visualize their behavior, and analyzing how they are used in various fields such as biology, economics, and physics. Applications could include modeling population growth, decay of radioactive materials, and the spread of diseases. The results of this analysis could be used to inform decision-making in these fields and to develop more accurate models for predicting future trends.

33 - Modeling the spread of a pandemic through a population and analyzing the effectiveness of different intervention strategies.

Develop a mathematical model that simulates the spread of the pandemic through a population, taking into account factors such as the transmission rate, incubation period, and recovery rate. The model could be used to predict the number of cases over time and the effectiveness of different intervention strategies, such as social distancing, mask-wearing, and vaccination. The model would need to be validated using real-world data and adjusted as new information becomes available. The results of the analysis could be used to inform public health policies and interventions to control the spread of the pandemic.

34 - Analyzing the behavior of different types of functions and their applications in science and engineering.

Conduct a study of different types of functions, such as linear, quadratic, exponential, and logarithmic functions, and their applications in science and engineering. This could involve analyzing real-world data sets and modeling them using different types of functions to determine which function best fits the data. The study could also explore the use of functions in fields such as physics, chemistry, and economics, and how they are used to make predictions and solve problems. The results of the study could be presented in a report or presentation, highlighting the importance of understanding the behavior of different types of functions in various fields.

35 - Analyzing the behavior of different types of numerical methods for solving differential equations and their applications in science and engineering.

Conduct a series of simulations using different numerical methods for solving differential equations, such as Euler's method, Runge-Kutta methods, and finite difference methods. The simulations could involve modeling physical phenomena such as fluid flow, heat transfer, or chemical reactions. The accuracy and efficiency of each method could be compared by analyzing the error and computational time for each simulation. The results could be applied to optimize numerical methods for solving differential equations in various scientific and engineering applications.

36 - Developing a model to predict the outcomes of a medical treatment based on patient data and medical history.

Collect patient data and medical history, including demographic information, medical conditions, medications, and treatment outcomes. Use statistical analysis and machine learning algorithms to develop a predictive model that can accurately predict the outcomes of a medical treatment based on patient data and medical history. The model would need to be validated using a separate set of patient data to ensure its accuracy and reliability. The model could then be used to inform medical decision-making and improve patient outcomes.

37 - Analyzing the behavior of different types of linear regression models and their applications in analyzing trends in public opinion polls.

Collect data from public opinion polls on a particular topic of interest, such as political preferences or social attitudes. Use different types of linear regression models, such as simple linear regression, multiple linear regression, and logistic regression, to analyze the data and identify trends and patterns. Compare the performance of the different models and determine which one is most appropriate for the specific data set and research question. The results of the analysis could be used to make predictions or inform policy decisions.

38 - Developing a model to predict the growth of a startup company based on market trends and financial data.

Collect market trend data and financial data for a range of startup companies. Use statistical analysis to identify patterns and correlations between the data. Develop a predictive model based on these patterns and correlations, taking into account factors such as industry trends, competition, funding, and management. The model could be tested and refined using data from existing startups, and could be used to make predictions about the growth potential of new startups based on their characteristics and market conditions.

39 - Studying the properties of different types of statistical distributions and their applications in analyzing public health data.

Analyze public health data using different statistical distributions such as normal, Poisson, and binomial distributions. This would involve understanding the properties and characteristics of each distribution and selecting the appropriate one based on the nature of the data being analyzed. The data could then be plotted and analyzed using statistical software to identify trends and patterns, and to draw conclusions about the health outcomes being studied. The results could be presented in the form of graphs, tables, and statistical summaries.

40 - Investigating the properties of different types of series and their convergence or divergence.

Conduct a series of tests on different types of series, such as geometric, arithmetic, and harmonic series. Use mathematical formulas and calculations to determine their convergence or divergence. Graphs and charts could be used to visually represent the data and make comparisons between the different types of series. The results of the tests could be analyzed to draw conclusions about the properties of each type of series and their behavior under different conditions.

41 - Analyzing the behavior of different types of functions and their limits.

Graph the different types of functions and analyze their behavior as the input values approach certain limits. This could involve finding the asymptotes, determining if the function is continuous or discontinuous at certain points, and identifying any points of inflection. The results could be presented in a report or presentation, highlighting the similarities and differences between the different types of functions and their limits.

42 - Investigating the properties of different types of sets and their relationships in set theory.

Conduct a comparative analysis of different types of sets, such as finite and infinite sets, empty sets, and subsets. Investigate their properties, such as cardinality, intersection, union, and complement. Use diagrams and examples to illustrate the relationships between the different types of sets. This analysis could be used to develop a deeper understanding of set theory and its applications in various fields.

43 - Exploring the properties of different types of number systems, such as real, complex, or p-adic numbers.

Conduct a literature review of the properties of different number systems and compile a list of key characteristics and equations. Then, design a series of mathematical problems that test these properties for each type of number system. These problems could include solving equations, graphing functions, and analyzing patterns. The results of these problems could be used to compare and contrast the properties of each number system.

44 - Developing a model to predict the behavior of a physical system using calculus of variations.

Collect data on the physical system being studied, such as its initial state and any external factors that may affect its behavior. Use the calculus of variations to develop a mathematical model that predicts the system's behavior over time. The model can then be tested against real-world observations to determine its accuracy and refine the model as needed. The final output would be a reliable model that accurately predicts the behavior of the physical system.

45 - Investigating the properties of different types of topological spaces and their relationships in topology.

Conduct a study of the different types of topological spaces, including Euclidean spaces, metric spaces, and topological manifolds. Analyze their properties, such as compactness, connectedness, and continuity, and explore how they are related to each other. This could involve creating visual representations of the spaces, such as diagrams or models, and using mathematical tools to analyze their properties. The results of the study could be used to better understand the fundamental principles of topology and their applications in various fields.

46 - Analyzing the behavior of different types of integrals, such as line integrals or surface integrals, and their applications in physics and engineering.

Conduct a literature review on the different types of integrals and their applications in physics and engineering. This could include researching the use of line integrals in calculating work done by a force field or the use of surface integrals in calculating flux through a surface. Based on the findings, develop a research question or hypothesis related to the behavior of a specific type of integral and its application in a particular field. Design and conduct an experiment or simulation to test the hypothesis and analyze the results to draw conclusions about the behavior of the integral and its practical applications.

47 - Developing a model to predict the behavior of a chemical reaction using chemical kinetics.

Collect data on the initial concentrations of reactants, temperature, and other relevant factors for the chemical reaction being studied. Use this data to develop a mathematical model that predicts the behavior of the reaction over time. The model could be tested by comparing its predictions to actual experimental data collected during the reaction. Adjustments could be made to the model as needed to improve its accuracy. The final model could be used to predict the behavior of the reaction under different conditions or to optimize reaction conditions for maximum efficiency.

48 - Investigating the properties of different types of algebraic structures, such as groups, rings, or fields.

Conduct a thorough literature review to gather information on the properties of different algebraic structures. Develop a clear research question or hypothesis to guide the investigation. Choose a specific algebraic structure to focus on and collect data by performing calculations and analyzing examples. Compare and contrast the properties of the chosen algebraic structure with other types of algebraic structures to draw conclusions about their similarities and differences. Present findings in a clear and organized manner, using appropriate mathematical language and notation.

49 - Analyzing the behavior of different types of functions, such as trigonometric, logarithmic, or hyperbolic functions, and their applications in science and engineering.

Conduct a study of the behavior of different types of functions, such as trigonometric, logarithmic, or hyperbolic functions, and their applications in science and engineering. This study could involve analyzing real-world data sets and identifying which type of function best fits the data. The study could also involve creating models using different types of functions to predict future outcomes or behavior. The results of this study could be used to inform decision-making in fields such as engineering, finance, or physics.

50 - Developing a model to predict the behavior of a financial market using mathematical finance.

Collect data on the financial market, such as stock prices, interest rates, and economic indicators. Use mathematical models, such as stochastic calculus and differential equations, to analyze the data and develop a predictive model. The model could be tested and refined using historical data and validated using real-time data. The output would be a model that can be used to predict the behavior of the financial market and inform investment decisions.

51 - Investigating the properties of different types of complex systems and their behavior, such as network dynamics, agent-based models, or game theory.

Develop a simulation model for each type of complex system being investigated. The model would need to incorporate the relevant variables and interactions between agents or components of the system. The behavior of the system could then be observed and analyzed under different conditions or scenarios. This would allow for a better understanding of the properties and dynamics of each type of complex system and how they may behave in real-world situations.

52 - Analyzing the behavior of different types of partial differential equations and their applications in physics and engineering.

Conduct a literature review to identify different types of partial differential equations and their applications in physics and engineering. Develop mathematical models to simulate the behavior of these equations and analyze their solutions using numerical methods. The results of the analysis could be used to gain insights into the behavior of physical systems and to develop new technologies or improve existing ones. Examples of applications could include fluid dynamics, heat transfer, and electromagnetic fields.

53 - Developing a model to predict the behavior of a fluid using fluid dynamics.

Use computational fluid dynamics software to create a model of the fluid system being studied. The software would simulate the behavior of the fluid under different conditions, such as changes in flow rate or temperature. The model could be validated by comparing its predictions to experimental data. Once validated, the model could be used to predict the behavior of the fluid under different conditions, such as changes in the geometry of the system or the addition of different chemicals. These predictions could be used to optimize the design and operation of the fluid system.

54 - Investigating the properties of different types of geometric objects, such as manifolds or curves, and their applications in geometry and physics.

Conduct a literature review to gather information on the properties of different geometric objects and their applications in geometry and physics. This could involve researching existing theories and models, as well as conducting experiments or simulations to test these theories. The findings could then be analyzed and synthesized to draw conclusions about the properties of different geometric objects and their potential applications in various fields. This could also involve developing new theories or models based on the findings.

55 - Analyzing the behavior of different types of stochastic processes, such as random walks or Markov chains, and their applications in probability theory and statistics.

Conduct simulations of different stochastic processes using software such as R or Python. Analyze the behavior of the simulations and compare them to theoretical predictions. Use the results to draw conclusions about the properties of the different stochastic processes and their applications in probability theory and statistics. Additionally, explore real-world examples of stochastic processes, such as stock prices or weather patterns, and analyze their behavior using the concepts learned from the simulations.

56 - Developing a model to predict the behavior of a biological system using mathematical biology, such as population dynamics, epidemiology, or ecology.

Collect data on the biological system being studied, such as population size, birth and death rates, and environmental factors. Use this data to develop a mathematical model that can predict the behavior of the system over time. The model can be tested and refined using additional data and compared to real-world observations to ensure its accuracy. This model could be used to make predictions about the future behavior of the system, such as the spread of a disease or the impact of environmental changes on a population.

57 - Investigating the properties of different types of wave phenomena, such as sound waves or electromagnetic waves, and their applications in physics and engineering.

Conduct experiments to study the properties of different types of wave phenomena, such as frequency, wavelength, amplitude, and speed. These experiments could involve using instruments such as oscilloscopes, microphones, and antennas to measure and analyze the waves. Applications of these wave phenomena could include designing communication systems, medical imaging technologies, and musical instruments. The results of these experiments could be presented in a report or presentation, highlighting the key findings and their significance in physics and engineering.

58 - Analyzing the behavior of different types of optimization problems in dynamic environments, such as optimal control or dynamic programming.

Conduct simulations of different optimization algorithms in dynamic environments, using various scenarios and parameters to test their performance. The results could be analyzed to determine which algorithms are most effective in different types of dynamic environments and under what conditions. This information could be used to develop more efficient and effective optimization strategies for real-world applications.

59 - Developing a model to predict the behavior of a social network using social network analysis, such as centrality measures, community detection, or opinion dynamics.

Collect data on the social network, such as the number of connections between individuals, the frequency and content of interactions, and any changes in the network over time. Use social network analysis techniques to identify patterns and trends in the data, such as the most influential individuals, the formation of subgroups or communities, and the spread of opinions or behaviors. Develop a model based on these findings that can predict future behavior or changes in the network. The model could be tested and refined using additional data or by comparing its predictions to real-world outcomes.

60 - Investigating the properties of different types of algebraic curves and surfaces, such as elliptic curves or algebraic varieties, and their applications in algebraic geometry.

Conduct a literature review to gather information on the properties of different types of algebraic curves and surfaces. Use mathematical software to generate and analyze examples of these curves and surfaces. Explore their applications in algebraic geometry, such as in cryptography or coding theory. Present findings in a research paper or presentation.

61. What are Interdisciplinary Approaches in Mathematics IA?

With the increasing focus on interdisciplinary learning, students are encouraged to link their Mathematics IA with subjects such as economics, environmental science, and computer science. This approach not only enriches the mathematical exploration but also allows students to showcase their ability to connect concepts across different fields.

How can I score highly?

Scoring highly in the mathematics internal assessment in the IB requires a combination of a thorough understanding of mathematical concepts and techniques, effective problem-solving skills, and clear and effective communication.

To achieve a high score, students should start by choosing a topic that interests them and that they can explore in depth. They should also take the time to plan and organize their report, making sure to include a clear introduction, a thorough development, and a thoughtful conclusion. The introduction in particular should demonstrate students’ genuine personal engagement with the topics.

An IB tutor in Hong Kong said:

"One important aspect that students ignore is that they should pay attention to the formal presentation and mathematical communication, making sure to use proper mathematical notation, correct grammar and spelling, and appropriate use of headings and subheadings."

Finally, students should make sure to engage with the problem and reflect on their own learning, and also make connections between different mathematical concepts and techniques. If they feel difficulty in these, then taking the help of an IB tutor can prove to be quite beneficial.

By following these steps, students can increase their chances of scoring highly on their mathematics internal assessment and contribute positively to their overall grade in the IB Mathematics course.

Need help from an expert?

The world’s top online tutoring provider trusted by students, parents, and schools globally.

Study and Practice for Free

Trusted by 100,000+ Students Worldwide

Achieve Top Grades in your Exams with our Free Resources.

Practice Questions, Study Notes, and Past Exam Papers for all Subjects!

Need Expert Help?

If you’re looking for assistance with IB Maths, get in touch with the TutorChase team and we’ll be able to provide you with an expert IB Maths tutor . We’ll be there every step of the way!

Professional tutor and Cambridge University researcher

Written by: Charles Whitehouse

Charles scored 45/45 on the International Baccalaureate and has six years' experience tutoring IB and IGCSE students and advising them with their university applications. He studied a double integrated Masters at Magdalen College Oxford and has worked as a research scientist and strategy consultant.

Related Posts

Is IB Maths Hard?

IB Chemistry IA: 60 Examples and Guidance

IB Physics IA: 60 Examples and Guidance

Hire a tutor

Please fill out the form and we'll find a tutor for you

• Select your country
• Afghanistan
• Åland Islands
• American Samoa
• Antigua and Barbuda
• Bosnia and Herzegovina
• Bouvet Island
• British Indian Ocean Territory
• Brunei Darussalam
• Burkina Faso
• Cayman Islands
• Central African Republic
• Christmas Island
• Cocos (Keeling) Islands
• Congo, The Democratic Republic of the
• Cook Islands
• Cote D'Ivoire
• Czech Republic
• Dominican Republic
• El Salvador
• Equatorial Guinea
• Falkland Islands (Malvinas)
• Faroe Islands
• French Guiana
• French Polynesia
• French Southern Territories
• Guinea-Bissau
• Heard Island and Mcdonald Islands
• Holy See (Vatican City State)
• Iran, Islamic Republic Of
• Isle of Man
• Korea, Democratic People'S Republic of
• Korea, Republic of
• Lao People'S Democratic Republic
• Libyan Arab Jamahiriya
• Liechtenstein
• Macedonia, The Former Yugoslav Republic of
• Marshall Islands
• Micronesia, Federated States of
• Moldova, Republic of
• Netherlands
• Netherlands Antilles
• New Caledonia
• New Zealand
• Norfolk Island
• Northern Mariana Islands
• Palestinian Territory, Occupied
• Papua New Guinea
• Philippines
• Puerto Rico
• Russian Federation
• Saint Helena
• Saint Kitts and Nevis
• Saint Lucia
• Saint Pierre and Miquelon
• Saint Vincent and the Grenadines
• Sao Tome and Principe
• Saudi Arabia
• Serbia and Montenegro
• Sierra Leone
• Solomon Islands
• South Africa
• South Georgia and the South Sandwich Islands
• Svalbard and Jan Mayen
• Switzerland
• Syrian Arab Republic
• Taiwan, Province of China
• Tanzania, United Republic of
• Timor-Leste
• Trinidad and Tobago
• Turkmenistan
• Turks and Caicos Islands
• United Arab Emirates
• United Kingdom
• United States
• United States Minor Outlying Islands
• Virgin Islands, British
• Virgin Islands, U.S.
• Wallis and Futuna
• Western Sahara

Your details

Alternatively contact us via WhatsApp, Phone Call, or Email

• [email protected]
• Get 21% OFF . Use the code: FIRST21

Mathematics: Analysis and Approaches IA Topics

Hello, IB scholars! As a seasoned IB writer, I’m here to guide you through the IB Mathematics Analysis and Approaches (IB Math AA) course, mainly focusing on the Internal Assessment (IA). In my experience, the IA is a crucial part of your IB Math AA, blending theoretical knowledge with practical application. Writing IB Math AA Internal Assessment is also challenging, so I will give you some IB Math AA IA ideas.

What Is IB Mathematics Analysis and Approaches?

IB Mathematics Analysis and Approaches (IB Math AA) is a course within the International Baccalaureate (IB) Diploma Programme, designed for students interested in developing their mathematics skills, particularly in the context of analysis and approaches. By the way, you can also read about the differences between IB Math IA and Math AA in our blog.

As I know from my experience, this course is well-suited for those who enjoy the challenges of solving complex problems and are interested in pursuing mathematics or related disciplines in higher education and their future careers.

IB Math AA emphasizes a thorough understanding of mathematical concepts, theories, and techniques. It includes topics like algebra, functions, calculus, and geometry, which are in-depth explored. The course is offered at two levels:

• Higher Level (HL) is more rigorous and includes additional topics and greater depth, making it suitable for students who might pursue mathematics, engineering, physical sciences, or economics in university.
• Standard Level (SL), while still challenging, covers fewer topics and is aimed at students who require substantial mathematics but not at the same intensity as HL.

The course places a strong emphasis on developing analytical and critical thinking skills. Students learn to approach complex mathematical problems systematically and develop and apply different problem-solving strategies.

A significant component of the course is the Internal Assessment , which is an independent, student-led project. The IA differs from Extended Essay and allows students to research an area of mathematics of personal interest, encouraging creativity and applying skills learned in the course.

IB Math AA prepares students for higher education, particularly in subjects that require strong analytical and mathematical skills. It’s recognized by universities for its rigor and depth, providing a solid foundation for further academic pursuits.

So, IB Mathematics Analysis and Approaches is a comprehensive, challenging course for students passionate about mathematics and its applications. It fosters a deep understanding of mathematical concepts and prepares students for further studies and careers where high-level math skills are essential.

You Might Also Like:

• How to Choose Math IA Topic
• IB Math IA Topics
• How to Get a Seven in IB Math AA
• Math SL IA Ideas
• 20 IB Chemistry IA Topics
• Physics IB IA Topic Ideas
• Computer Science IB IA Topics
• Economics IA Topic Ideas
• Geography IA Ideas

IB Math AA IA Ideas and Topics

According to general IB criteria, an ideal topic should be challenging and accessible. It means balancing complexity with your skills and resources. Also, remember the IB Math AA IA topic should allow for thorough mathematical research. Below are some IB Math AA IA ideas you can consider.

Standard Level (SL) IB Math AA IA Ideas

For Standard Level (SL) students, real-world applications are a goldmine. Topics like sports statistics or architecture geometry can be engaging and informative. Also, remember creativity is your ally. Even standard topics can become intriguing with a unique angle.

• The Mathematics of Credit Card Interest . How does compound interest affect the long-term cost of credit card debt?
• Statistics in Sports: Analyzing Player Performance . Can statistical models accurately predict a basketball player’s performance based on past game data?
• Geometry in Architecture . How are geometric principles used in the design of modern buildings?
• The Fibonacci Sequence in Nature . How accurately does the Fibonacci sequence predict natural patterns, like the arrangement of leaves or seeds?
• Calculus in Medicine: Drug Concentration Over Time . How does calculus model the decreasing concentration of a drug in the bloodstream over time?
• Mathematics of Music: Frequencies and Ratios . What is the relationship between frequency ratios and musical harmony?
• Projectile Motion in Physics . How does calculus help in predicting the trajectory of a projectile?
• Statistics and Climate Change . Can a statistical analysis of temperature data over the past 50 years predict future climate trends?
• Golden Ratio in Art and Design . How is the golden ratio applied in famous artworks and designs?
• The Math Behind Voting Systems . How do different voting systems affect the outcome of elections?
• Probability in Games of Chance . What is the probability of winning in a specific card game, and how can strategies be optimized?
• Mathematics of Population Growth . How can mathematical models predict population growth in a specific region?
• Optimization in Business: Minimizing Costs . How can calculus be used to minimize production costs in a manufacturing business?
• Mathematics of Loan Amortization . How does an amortization schedule break down loan payments into interest and principal?
• Statistical Analysis of Consumer Behavior Trends . Can statistical methods predict future consumer behavior based on past purchasing data?
• Mathematical Exploration of Stock Market Trends . Can mathematical models identify patterns in stock market fluctuations?
• Calculus in Environmental Science: Carbon Footprint Analysis . How can calculus be used to model the change in a city’s carbon footprint over time?
• Probability in Genetics: Mendelian Inheritance . What is the probability of inheriting specific genetic traits according to Mendel’s laws?
• The Math Behind Cryptocurrencies . How does the underlying mathematics of blockchain technology ensure security in cryptocurrencies?
• Ratios in Photographic Composition . How do ratios, such as the rule of thirds, enhance composition in photography?
• Mathematical Patterns in Historical Architecture . What mathematical patterns are evident in the architecture of ancient civilizations?
• Statistics in Healthcare: Analyzing Patient Data . Can statistical analysis of patient data predict disease outbreaks?
• Applications of Logarithms in Astronomical Calculations . How are logarithms used in calculating distances of celestial bodies?
• Mathematical Models in Sports Strategy . How can mathematical models improve decision-making in team sports strategies?
• Geometry of Shadows: Understanding Eclipses . How does geometry explain the occurrence and patterns of solar and lunar eclipses?
• Application of Probability in Insurance . How do insurance companies use probability to calculate premiums?
• Mathematics in Cooking: Ratios and Proportions . How are ratios and proportions critical in creating culinary recipes?

These IB Math AA IA ideas and research questions aim to inspire your exploration, combining theoretical knowledge with practical application in diverse fields.

Get Help With Your Paper

Higher level (sl) ib math aa ia ideas.

For Higher Level (HL) students, the challenge intensifies. Your IA should reflect a deeper understanding of complex concepts. Think about integrating advanced calculus or algebra in real-world scenarios or theoretical problems.

• Non-Euclidean Geometry: Exploring Hyperbolic Space . How does hyperbolic geometry differ from Euclidean geometry in the representation of space?
• Advanced Calculus in Economics: Market Equilibrium . How can differential calculus be used to find the market equilibrium point?
• Fractal Geometry in Nature . How do fractal dimensions provide a measure of complexity in natural patterns?
• Complex Numbers in Electrical Engineering . How do complex numbers model alternating current circuits?
• Game Theory in Economics . How can game theory explain decision-making in oligopolistic markets?
• Cryptography: RSA Encryption . How does the RSA algorithm use prime numbers for secure communication?
• Fourier Series in Signal Processing . How does the Fourier series decompose complex signals into constituent frequencies?
• Chaos Theory in Meteorology . How does chaos theory explain the unpredictability of weather patterns?
• Monte Carlo Simulations in Risk Analysis . How can Monte Carlo simulations predict risk in financial investments?
• Topology and Its Applications . How does topology explain properties of space that are preserved under continuous deformations?
• Linear Algebra in Computer Graphics . How is linear algebra used in creating 3D computer graphics?
• Mathematical Modeling of Epidemics . How can mathematical models predict the spread of an infectious disease?
• Calculus of Variations in Physics . How does the calculus of variations contribute to understanding the principles of classical mechanics?
• Numerical Methods in Engineering Problems . How are numerical methods used to solve non-linear equations in engineering?
• Statistics: Regression Analysis in Market Research . How can regression analysis predict consumer behavior based on historical data?
• Advanced Probability in Genetics: Beyond Mendelian Inheritance . How can advanced probability models explain genetic inheritance patterns that deviate from Mendel’s laws?
• Graph Theory in Optimizing Transportation Networks . How can graph theory be applied to optimize public transportation networks?
• Differential Equations in Population Dynamics . How do differential equations model predator-prey dynamics in an ecosystem?
• Number Theory in Cryptography Beyond RSA . What are the mathematical principles behind modern cryptographic algorithms beyond RSA?
• Vector Calculus in Physics: Electromagnetic Fields . How does vector calculus describe the behavior of electromagnetic fields?
• Mathematical Logic and Its Applications in Computer Science . How does mathematical logic underpin the algorithms used in artificial intelligence?
• Advanced Statistics in Psychological Research . How can advanced statistical methods improve the reliability of psychological studies?
• Linear Programming in Resource Allocation . How does linear programming solve complex resource allocation problems in industries?
• Quantum Mechanics: Mathematical Foundations . What are the key mathematical principles underlying quantum mechanics?
• Mathematical Analysis of Renewable Energy Systems . How can mathematics optimize the efficiency of renewable energy systems?
• Game Theory in Political Science . How does game theory apply to decision-making processes in political science?
• Analyzing Financial Markets with Stochastic Processes . How do stochastic processes model the unpredictable nature of financial markets?

These IB Math AA IA ideas provide many opportunities for HL students to explore mathematical concepts in practical and theoretical contexts.

The Bottom Line

In conclusion, dear students, consider your IB Math AA IA an exceptional platform to display your proficiency and passion for mathematics. Approach this task with eagerness and thoroughness. Based on my extensive experience, a carefully planned IA can fulfill your IB experience. I wish you the best of luck, and may your mathematical investigations bring remarkable findings! Also, remember that our  IB IA Writing Service  experts are here to help you.

Nick Radlinsky

Nick Radlinsky is a devoted educator, marketing specialist, and management expert with more than 15 years of experience in the education sector. After obtaining his business degree in 2016, Nick embarked on a quest to achieve his PhD, driven by his commitment to enhancing education for students worldwide. His vast experience, starting in 2008, has established him as a reputable authority in the field.

Nick's article, featured in Routledge's " Entrepreneurship in Central and Eastern Europe: Development through Internationalization ," highlights his sharp insights and unwavering dedication to advancing the educational landscape. Inspired by his personal motto, "Make education better," Nick's mission is to streamline students' lives and foster efficient learning. His inventive ideas and leadership have contributed to the transformation of numerous educational experiences, distinguishing him as a true innovator in his field.

Tips for Writing a High-Scoring IB Essay

The IB rewards essays that are focused, analytical, and well-structured. In this guide, we’ll share practical tips for success, from using evidence effectively to polishing your arguments through thoughtful revisions.

The Benefits of Joining IB Study Groups

You may change the way you tackle the demanding requirements of the IB program by joining an IB study group. These groups provide a collaborative learning environment in addition to sharing notes and study sessions.

How to Handle Stress and Pressure During IB Exams?

Dealing with the stress and pressure of IB exams can be challenging, but it’s manageable with the right strategies. In this article, I’ll give you practical tips on how to stay calm and focused during exam season. From setting up a balanced study routine to developing a positive mindset and using effective stress reduction techniques, these methods will help you approach IB exams with confidence.

The Role of TOK in Interdisciplinary Understanding

TOK encourages students to look into how different types of information connect and combine, which leads to a more all-around way of learning. TOK acts as a link between subjects that might otherwise seem unconnected, such as relating mathematical ideas to natural patterns or examining the moral ramifications of science developments.

How to Conduct Effective Peer Reviews in IB Projects?

Peer review in IB projects is a vital skill that can greatly improve the quality of your projects and your academic growth. From what I’ve seen, peer reviews are a great way to get helpful feedback, see things from different angles, and make your work better.

Utilizing Digital Tools for IB Study and Research

Now that we live in a digital world, using technology to its fullest can greatly improve your IB study and research. Staying prepared, controlling time, and conducting research have never been simpler thanks to the abundance of apps and platforms available. The important thing is to know which tools will help you reach your school goals.

© 2024  I Bstudenthelp.com. This website is owned and operated by Udeepi OU Harju maakond, Tallinn, Lasnamäe linnaosa, Sepapaja tn 6, 15551. Disclaimer : Services we provide are only to assist the buyer like a guideline to complete any kind of writing assignment. Privacy Policy Terms and Conditions Cookie Policy Revision Policy Refund Policy

• Find A Tutor
• Geneva Tutors
• Lausanne Tutors
• Zurich Tutors
• Basel Tutors
• Online Tutors
• Maths Tutors
• Chemistry Tutors
• Physics Tutors
• Biology Tutors
• English Tutors
• History Tutors
• Geography Tutors
• Language Tutors
• Special Educational Needs
• Residential Tutors
• Primary School
• School Entrance Exams
• Middle School
• Combined Science
• Maths AA and AI
• IB Internal Assessment
• Environmental Systems & Societies (ESS)
• Sports, Exercise & Health Science
• Computer Science
• Global Politics
• Digital Society
• Business Management
• Visual Arts
• English A/B
• English Oral (IO)
• German Oral (IO)
• French Oral (IO)
• Spanish A/B
• French Ab Initio
• German Ab Initio
• Spanish Ab Initio
• IB Extended Essay
• IB Theory of Knowledge
• University Applications
• Our Approach
• Happy Parents
• School Choice
• Become a Tutor

50 Unique IA Maths Topics Ideas that Actually Work

By TutorsPlus

Internal Assessment (IA) is a crucial component of your IB Maths journey. As exciting as an independent investigation may be, many struggle from the very beginning: finding the perfect topic is harder than it seems. If you’re one of these students, we’re happy to offer a few fresh IA Maths ideas you can try.

From algebra and geometry to calculus and statistics, these ideas should spark your inspiration and help you approach your IA research project with confidence.

Why it is important to choose unique IA Maths Topics Ideas

Below, you will find 50 diverse IA Maths topics to spark your creativity for the Internal Assessment. Remember, these are just starting points, not blueprints. Copying a title and question directly is not the best approach.

Firstly, thousands of IB students worldwide submit IAs, and your teacher has likely seen similar ideas before. You need to make sure your topic and research question is unique to you to demonstrate independent thinking and effort. What’s even worse, direct copying violates academic integrity. In fact the IB view this as plagiarism.

Nevertheless, these 50+ IA Maths ideas can serve you well as examples to help you come up with your own ideas. You just need to incorporate specific details (location, time frame, or additional factors) to personalise the topic. For example, instead of simply “Modelling the spread of infectious diseases,” you could explore:

• Modelling the spread of influenza in London during winter 2024-2025.
• Prediction of the spread of COVID-19 in densely populated areas compared to rural areas during future outbreaks.
• Analysing the effectiveness of different social distancing measures in controlling the spread of a disease in a specific country.

However, if you’re not inspired by any of the topics or want to figure out how to choose a topic on your own, use our guide – How to choose your Maths IA topic .

IA Maths Ideas You Can Try

Without further ado, let us provide dozens of IA Maths ideas that can help inspire you to write a high-scoring research report.

Modeling and Simulation

• Modeling the spread of infectious diseases. You can explore different models (e.g., the SIR model) and analyse their effectiveness in predicting real-world scenarios.
• Optimizing resource allocation in disaster relief . Apply mathematical modelling to determine the most efficient distribution of resources in response to natural disasters.
• Modelling population growth and sustainability . Explore different models for population growth and analyse the implications for sustainability.
• Simulating Manhattan Traffic with Agent-Based Modelling . Apply program agents with rules to simulate realistic traffic flow in Manhattan.
• Modelling Soccer Ball Trajectories with Calculus . Use calculus and physics to model the flight of kicked soccer balls.
• Modelling Predator-Prey Dynamics with Differential Equations . Use differential equations to model the cyclical relationship between a predator and prey population.
• Applying Trigonometric Functions to Model Planetary Motion . Investigate the role of trigonometric functions to model the orbits of celestial bodies and to predict their positions and movements over time.
• Exploring the Connection between Differential Equations and Population Dynamics . Analyse the maths behind the models of population growth, decay, as well as interactions between different species. Explain the role of predictions in determining population trends.

Data Analysis and Statistic

• Analysing voting systems and their fairness . Analise different voting systems (e.g., ranked-choice, instant-runoff) and evaluate their mathematical properties for fairness.
• Analysing sports statistics and predicting performance . Investigate how statistics are used in sports to analyse past performance and predict future outcomes.
• The mathematics of fairness in elections . Analyse different apportionment methods (e.g., Hare quota, Saint-Lague method) and their implications for political representation.
• The mathematics of social media algorithms . Analyse how algorithms are used to personalise and recommend content on social media platforms.
• Analysing the Impact of Probability and Statistics in Sports Analytics . Explore the application of probability and statistics to analyse various aspects of sports, for instance, player performance. How can mathematics help predict game outcomes as well as make informed decisions in sports betting and team management?
• Using Statistics to Evaluate the Effectiveness of Medical Treatments . Explore how statistics helps to design clinical trials, analyse medical data, as well as evaluate the efficacy and safety of medical treatments.
• Predicting NBA Player Performance Through Regression Analysis . Analyse sports data sets to identify trends and make predictions.
• Analysing Risk Using Markov Chains . Implement Markov chains to analyse risk and probability scenarios.
• Analysing the Impact of Probability and Statistics in Quality Control . Investigate how product quality monitoring, defect identification, and standard compliance can benefit from probability and statistics.

Applied Mathematics

• The mathematics of fair division problems . Explore different methods for dividing resources fairly (e.g., the “cake-cutting” problem) and analyse their properties.
• Exploring the Applications of Linear Programming in Supply Chain Management . Investigate how linear programming can optimise inventory levels, production schedules, as well as transportation routes to reduce costs and improve efficiency in supply chains.
• Applying Calculus to Optimise Travel Routes and Logistics . Analyse how to determine the most efficient travel routes taking into account factors such as distance, travel time, fuel consumption, and traffic conditions.
• Applying Calculus to Optimise Investment Strategies in Finance . Analyse the application of calculus in various investment strategies such as portfolio allocation or risk management. How can they help maximise returns on investments?
• Applying Linear Programming to Optimise Production Schedules in Manufacturing . Analyse how linear programming can optimise production schedules, minimise production costs, and improve efficiency in manufacturing processes.
• Finding shortest paths using graph theory . Find the shortest path between two points on a map using graph theory.
• Finding the Optimal Bus Routes in London Using Graph Theory . Explain how to find the shortest path between two points on a map using graph theory.
• Portfolio Optimization with the Markowitz Model . Use the Markowitz model to construct optimal investment portfolios.
• Utilising Vectors to Analyse Forces and Equilibrium in Engineering. Analyse how one can use vectors to represent forces acting on objects. Additionally, determine the conditions for equilibrium in mechanical systems.
• Investigating the Role of Calculus in Optimising Renewable Energy Production . Analyse how calculus can be used to determine the optimal tilt angle of solar panels, the ideal size of wind turbines, as well as the best locations for hydroelectric power plants to maximise energy production.

Practical Math

• Mathematical modelling in finance . Explore how mathematics is used in finance, such as pricing options, calculating loan payments, or managing risk.
• The Monty Hall problem and probability in decision-making . Explore the Monty Hall problem and apply concepts of conditional probability to real-world scenarios.
• The mathematics of optimal packing . Analyse different strategies for packing objects efficiently in various contexts (e.g., sphere packing, bin packing problem).
• Analysing the Role of Probability in Predicting Weather Patterns . Investigate how probability is used in weather forecasting to predict the likelihood of precipitation, temperature, wind speed, and other weather conditions.
• Investigating the Use of Matrices in Image Processing and Computer Graphics . Explain the role of matrices underlying image processing techniques such as filtering, compression, and enhancement.
• The mathematics behind machine learning algorithms . Explain how machine learning algorithms work by exploring the underlying mathematical concepts (e.g., linear regression, gradient descent).

Geometry and Visualisation

• Fractal geometry in nature . Analyse the self-similar patterns of fractals found in natural phenomena like coastlines or snowflakes.
• Exploring the Relationship between Topology and Graph Theory . Investigate the connections between topology and graph theory, and how they can be applied to analyse networks, maps, and other structures.
• Modelling Romanesco Broccoli Fractals with L-Systems . Use L-systems to generate and analyse fractal patterns.
• Analysing Alhambra Tiling Patterns . Use geometry to study and recreate intricate tile patterns.
• Applying Linear Algebra to Model Electrical Circuits . Investigate how linear algebra can be used to analyse electrical circuits, determine current and voltage distributions, and design efficient electrical systems.
• The mathematics of computer graphics . Explore how mathematical concepts like 3D transformations and ray tracing are used to generate computer graphics.
• The Use of the Golden Ratio in Art and Nature . Investigate occurrences of the golden ratio in art, architecture, and nature.
• Exploring the Relationship between Complex Numbers and Fractals . Investigate the connection between complex numbers and fractals. How can complex numbers be used to generate and analyse intricate geometric patterns?
• The mathematics of music: Exploring scales, chords, and musical harmony. Analyse the mathematical relationships between notes, scales, and chords in music theory.

Number Theory and Carthography

• Cryptography: Breaking simple ciphers and analysing encryption algorithms . Analyse different encryption techniques and explore strategies for breaking simple cyphers.
• The mathematics of cryptography : Exploring public-key cryptography and its applications. Analyse public-key cryptography and its importance to secure communication (e.g., RSA encryption).
• Investigating the Applications of Number Theory in Cryptography . Analyse encryption and decryption algorithms that use number theory. How can it help ensure the security of digital communications?

Game Theory

• The mathematics of games and puzzles . Analyse the strategies and mathematical principles behind popular games like Sudoku or Rubik’s Cube.
• Investigating the Applications of Game Theory in Economics and Politics . Explore how game theory can predict the outcomes of competitive situations and impact strategic decision-making.
• The mathematics of voting systems and strategic voting . Explore how strategic voting can influence the outcome of elections and analyse its implications for different voting systems.

Chaos Theory

• Exploring chaos theory and its applications . Investigate the unpredictable behaviour of complex systems and their applications in various fields (e.g., weather forecasting, economics).
• Analysing the Impact of Chaos Theory in Weather Prediction . Investigate how chaos theory affects weather prediction, and how it can be used to improve the accuracy of long-term weather forecasts.

IA Maths Topics: Conclusion

With a good Maths IA topic idea, you’ll be well on your way to conducting a successful independent investigation. Sometimes, however, even the greatest ideas require extra help to turn into well-written project reports. If you, too, struggle at any stage of your exploration, don’t hesitate to reach out to TutorsPlus.

Our team of experienced IB Maths tutors can provide guidance and support throughout the entire process. You can count on us to refine your topic and organize your IA Maths ideas into logical and well-structured writing. Additionally, we can provide feedback as well as resources to improve your mathematical skills.

Feel free to contact TutorsPlus at 022 731 8148 and [email protected]. We are always here to help you make the most of your IB experience.

Sara has been an education consultant for TutorsPlus for 15 years, and is an expert on international IB education.  She is also a parent of two lively children.

Find a Tutor

Popular Posts

English IO – How to Ace Your IB English Literature & Language Oral

Tips to Get a Top Grade in Your IGCSE English

How to get a top score in your IB TOK Exhibition

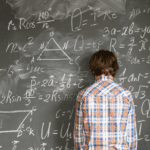
IGCSE Maths Revision Tips To Help You Today

What is the IA, EE or TOK? Everything you need to know about the IB written assignments

Maths Anxiety – How Parents Can Help 

More articles from our expert tutors.

Free webinar – Standing out from the Crowd: How to impress US universities with your application

10 Tips For Success in the IB English IO

Oxbridge Interview Tips & Tricks

Find a Tutor Today

" * " indicates required fields

Step 1 of 5

Find the best support for your family

• Customer Reviews
• Extended Essays
• IB Internal Assessment
• Theory of Knowledge
• Literature Review
• Dissertations
• Essay Writing
• Research Writing
• Capstone Projects
• College Application
• Online Class

The Definitive Guide to Choosing the Best IB Mathematics IA Topics

45  Comments

by  Antony W

August 19, 2022

Imagine you were fascinated by the shape of nuclear reactor chimneys, called Natural Draft Cooling Towers. What an odd shape, you think (a hyperboloid, if you’re wondering). But how would you find out why they are so shaped? As it turns out, mathematics is a beautiful, fascinating language you can use to describe something like that. And when you explore such a personally fascinating subject within certain regulations of the IB, you will be writing your mathematics internal assessment.

As you can deduce, the IB math internal assessment is all about exploring mathematically a subject of personal interest. How well you do that and present your process determines how many marks out of the total 20 you will receive. However, most students live in mortal fear or both the IB math exam and the internal assessment.

If you are one such student, fear not. This detailed guide will teach you how you need to approach the math assessment by choosing the right topics, as well as how to make a top-grade essay. You can also get further IB guides in full detail here on our blog.

The team at Help for Assessments is also ready to give more than just passive “how to” assistance. Let us take the IB internal assessment nightmare away from you and write the essay for you. Our highly skilled and experienced team assures you of top-notch work, original and flawless in research and quality. All these at the best rates, so don’t hesitate to give us your order. We will even give you 25% off your first order to get you started.

Do you still want to push on? This article will give you all you need to choose suitable topics for your maths IA, explore what the test is about, and finish with some fresh sample idea topics for the math IA.

Struggling to pick your Math IA or AA topic? 

What the IB Maths Internal Assessment Topics All About

The mathematics internal assessment is about exploring the math behind a topic of interest, then presenting the whole thing in the form of a short thorough report. Ideally, the topic should be completely original and serve to prove that you have a firm grasp of mathematical concepts, principals, and knowledge.

According to the IA mathematics rubric, the IBO is looking for the following in a good essay:

• Communication : Communication measures how well you organize and explain your exploration. It must be logically developed and coherent. The essay generally should have three parts: an introduction, the rationale or explanation, and a conclusion.
• Mathematical presentation:  You need to use appropriate mathematical languages, with the right formulae, diagrams, tables, charts, models, and other figures as needed.
• Personal engagement:  This is a measure of the level to which the student interacts with the subject matter on a personal level. It is more than being original or authentic with the idea - it has to stem from some experience in your life or one you have direct links with.
• Reflection:  This criterion assesses how the student reviews and analyzes the problem and its solution in the exploration.
• Use of mathematics:  This is self-explanatory - how well does the student use the concepts, knowledge, and skills gained in their respective mathematical level so far?

Thus, the maths IA is about displaying your ability to apply abstract concepts and knowledge in math to a real-world situation and communicating clearly to your audience. In this case, the audience is your instructor/professor, and writing a good IA essay starts from picking the right topic.

Not sure whether to order Math IA or AA? Click below to see our latest samples! 

What Makes a Good Math IA Topic

A good topic for the IB mathematics internal assessment is one that allows you to fulfill all the above requirements. It will help you explore an area of interest deeply and exhaustively, while at the same time providing an avenue for you to put your acquired mathematical skills into good use.

If you are to be successful in these goals, your essay should have certain important qualities. These are the same qualities your topic should have:

• Simple and clear language: The rule of thumb is that everyone in your age group (your classmates) must be able to understand your essay. Thus, your topic needs to be simple. A complex subject will be hard for you to write, tough to break down into manageable bites, and ultimately cost you valuable marks.
• Concise and well-focused: The essay will be 6-12 pages in length, so you need to have a topic that can be exhaustively examined in that range. As is said in other IB assessments, the topic should be specific but not too narrow that it restrains or limits you. For example, our chosen problem of the nuclear reactor exhaust steam funnels could be confined to modeling the hyperboloid shape of the cooling towers and start from there.
• Interesting : The chosen topic needs to be exciting enough to elicit not only your interest but that of your audience. It needs to be one that is naturally intriguing to warrant a 12-page study into its underlying mathematical principles.
• Fresh : By fresh, we mean a relatively unexplored topic. Too many students do game theory, but that topic has been gone through by thousands of students in decades of consecutive years. Don't do that - go for something fresh, or seek to add an extra twist to something that already exists.
• Has clear connections with one or more mathematical fields: Your chosen topic should be based on a given mathematical area, or rely on a few of them. Drawing connections between different areas, e.g. Calculus and geometry will impress your instructor. However, always keep it within your attained academic level.

With the goal in mind, it's time to look into the process that precedes choosing a perfect math IA topic.

How to Choose a Mathematics IA Topic

Most math gurus insist that math is not just an abstract subject. It has real and effective links to the real world, and that is what the whole point of the internal assessment is.

To choose the topic, start with the real-life experiences to help you pinpoint an area of math you want to explore.

The following steps will help you:

• Brainstorm:  The first hurdle is to find a general area of interest, which ideally should be related or founded on your interests. For example, if you love medicine and want to study it in the future, you can start with a certain field that fascinates you. Future lawyers, businessmen, engineers, and IT enthusiasts can all find something intriguing to pursue.
• Narrow down: With the first few ideas, the next step is to find a topic that has a lot of mathematical potential. You will find that reading lots of journals, watching videos, and talking with friends gives you lots of seed ideas for this stage.
• Evaluate: Evaluate each of the ideas you have on the strength of the qualities above. Is it relevant? Simple enough for your level? Exciting? Will it be useful to you in your career or your life?
• General research: General research into the mathematics involved in your chosen topic will help you determine what you need to learn and determine how feasible your topic is. The point here is to find out if the topic is right for you, and whether you can find the right material to base your exploration on.
• Come up with a working research question: Every IA needs to have a research question to streamline the exploration and provide direction to the essay. As with the topic, the research question needs to be specific but just wide enough to give you enough material to fill the said 6-12 pages.

Or the other hand, perhaps this topic would be better suited to the Physics IA? It’s up to you!

Do you need help with your Math IA or AA? 

30+ Math IA Topics for SL and HL Levels

We’ve been writing IB Math IA assignments for over 5 years. From a professional academic writing assistance point of view, the number one challenge that many IB learners have is topic selection.

On the surface, Math IA is about investigating concepts within a topic of interest and presenting your findings in a 2,200-word report.

In practice, coming up with an original topic, which you can investigate to prove that you have a strong grip of mathematical concepts and principles can be somewhat challenging.

In this section, we put together a list of 20+ IB Math IA topic for SL and HL to help you understand what good topic looks like based on the selection criteria that we’ve shared in this guide.

• How accurate are mathematical predictions for events with a low likelihood but huge impact?
• Considering the risks involved in making decisions based on incomplete or conflicting information might make us more cautious.
• How do normal numbers fare when compared to random number generators?
• Create a virtual version of the disaster at Chernobyl and its subsequent effects on Japan.
• Do the numbers that make up a Pythagorean triple follow any kind of regularity?
• Does a high degree of association exist between BMI and GDP per capita?
• What kinds of character combinations are best for online safety in light of brute force attacks?
• To what extent does Bayesian probability work in a real-life setting and is it possible to add complexity to it?
• How do those involved in pyramid schemes or other forms of fast-paced fraud use mathematics to amass huge fortunes so quickly?
• Determine the climber's fall severity by measuring the distance from the final point of connection.
• Is it feasible to forecast the outcome of athletic events using a Poisson model and some familiarity with Excel?
• How long would it take someone to try to guess someone else’s password? What's the deal with adding symbols and digits to a password?
• How can we identify individual tones using sine waves of different frequencies?
• Is there a way to utilize arithmetic to predict how contagious diseases like measles will move across a population?
• Do large transfer window expenditures result in a higher victory percentage a sports season?
• With what method of voting can the most people be certain that their preferred candidate will win the election?
• A study of the geometric sequence's connection to the camera's aperture
• How well do you think integration would work to determine the gini coefficient for a sample of nations, allowing you to make reliable comparisons of the economic inequality between them?
• Find out if there's a correlation between music and fractions, or see if this series converges.
• If a fatal flu virus were to sweep the globe, how long do you think it would take humanity to perish?
• Examine the ratios of frequencies between notes to see why some do not sound good together while others do.
• What kinds of numbers have the most bearing on a basketball team's success?
• A look at how uncertainty about the future might make people more risk-averse and how asymmetric information plays a role in this phenomenon.
• The ideal amount of force and launch angle for a javelin or shot put world record throw.
• The gravitational attraction of other things in space causes the orbits of planets and comets to be elliptical. Look into the field of space exploration!
• Study the numbers behind the processes of heredity and natural selection.
• How can we utilize computers to learn more about sequences?
• Is it possible to employ computational methods in addition to pure mathematics to find an answer?
• Applying the mechanics of fast-moving spacecraft to the problem of interstellar travel
• Applying quantum mechanics, we may examine the universe's innate probabilistic character.
• If it takes the tortoise twice as long to cover the same distance as a runner, then there's no way the runner can catch up to it no matter how fast he runs.
• Using tools from probability and game theory, researchers investigate the most effective bluffing techniques for poker.
• Does the time it takes a kid to arrive to school depend on how far they live from the school?
• Check out the Guardian Stats to see if the top teams in the league are also the ones that commit the most fouls.

Tips to Help You Write the Best Math IA Assignment

The following tips can help you write a more comprehensive IB Math IA assignment:

1. Choose a Topic You’re Interested In

Since you will be working on your Math IA for a few months, it would be preferable if you choose a topic that genuinely interests you, rather than one that is simply required.

2. Use a Simple Language

Ensure that language is exact, clear, and succinct. Write your IA in a way that anybody of your age can read and understand.

Choosing a complicated topic may result in a disorganized and difficult-to-understand IA, so try to avoid doing so. Also, avoid writing lengthy accounts of your own experiences. This is the requirement for "Communication" on the math IA.

3. Use Appropriate Terms

Use appropriate mathematical notation and symbols throughout your IA report.

To properly format all mathematical symbols, use MathType or a comparable program for mathematical expressions. Doing so will enhance clarity and will get you easy points for "Mathematical Presentation"

IB also requires you to reflect on your findings in the report as part of your IA. Comment (thoughtfully), but avoid paraphrasing the results.

Describe some of the insights you've acquired from the IA mathematical conclusion. The greater the depth of your contemplation, the more points you will receive for the "Reflection" criterion.

Do You Need Help With Your IB Math Internal Assessment?

The mathematics internal assessment requires an astute mind to complete, and choosing the topic is the least of your worries. Many students are scared stiff on its account, but you don’t have to be. Help for Assessment is here to help you pass the internal assessment in maths, and not just because of this guide. The team here is made up of top IB experts who will do the internal assessment for you upon request. All you have to do is leave us your order here , and we guarantee you top grades and 100% original, impeccably researched, and fully proofed work. Of course, confidentiality is guaranteed, no matter where you come from. 

About the author 

Antony W is a professional writer and coach at Help for Assessment. He spends countless hours every day researching and writing great content filled with expert advice on how to write engaging essays, research papers, and assignments.

Leave a Reply

Your email address will not be published. Required fields are marked *

I need help finding a math ia topic related to cars as its my interest but i am very confused and need some guidance

Hello Muhannad.

Thanks for reaching out. We’re happy to help. One of our representatives will get back to you via e-mail shortly. Thank you.

I need help in deciding a viable topic for my math is. I am very interested in cryptocurrency, the stock market, cricket, exercise, video games. Anything, but guidance would be highly appreciated.

Thanks for reaching out. We’re happy to help. One of our representatives will get back to you via your email for further assistance

Hi there, can you provide some help regarding math IA topics? I am a bit interested in the billiards topic and the math behind billiards, is the mathematics in billiards hard? or else I would like to use your help to choose a topic that has easy maths as I am an application student standard level, thank you for your coordination.

Hi, I stuck in choosing the best topic inline with the 3D shapes, for my exploration . Would you please assist me?

I am not really sure where to start for this IA. I am interested in the piano and music, however there have been past IAs on that. I don't know what else to think of.

I need help finding a math ia topic related to medicine and business

hi i need to find a topic and a research question that I am interested in. i have a few ideas but it is hard to narrow it down

Hey, I'm in need of some help finding an IA topic related to cars and I'm not sure where to start or what to do

Hi, I am Dina I need help in deciding my IA topic. I'm more concerned with the medical field and pharmacokinetics of medicines.

Hi, I would like to engage Mr. Anthony W for IB IA topic for Math AA HL for my son. Appreciate if you can get in touch wtih me at the earliest.

Hi, I need help in finding a topic about my math IA, I'm interested in the statistics and probabilities of winning a sneaker raffle. But I don't know how to do the maths of it.

Good day, I am currently struggling to come up with a math IA. I would like to do my exploration around medicine or something relating to careers. I currently have a few ideas about what I want to do, but I am in need of some assistance.

I need help finding a math IA HL topic related need some guidance.Please help me

I need help finding a math analysis and approach IA HL topic related need some guidance. Please help me

I need help in Maths IA for HL maths. How to go about to seek help?

I need a math IA topic that is related to statistics and could include something that is easy to find data for. I was thinking traffic flow, yet I don't know where to get the data from.

Hey, I have an research question for maths, but I not sure how to start it. Will someone be able to help me out?

I need to find my IA topic based on an example of how mathematics apply to real life

Hi! I need some assistance in finding an IA topic and the math. I am thinking of how essential immigrant workers are to the community and how without them especially during the pandemic, affects the food industry. I am not sure what kind of math I would have to be doing. Can you please help me?

Please help me choose an IA topic !!

Kindly read this guide carefully again. It should help you choose an IA topic for your next assignment.

i clearly don't know what to choose for my IA I don't really have some favorite stuff but I play basketball by myself not within a team or I thought if I can do an IA about coffee because I drink a lot of different types of coffee but in the same time I want a great IA that interests the person that is gonna read it

i need a ia topic and writing it

I need help finding a math ia topic related to keyboards or computers related. I was wondering if you can reach back to me immediately and we can talk about it? Thank you

Hello, I want to write a maths IA about Scouts because I was a scout and I am interested in scouts. I am finding it difficult to relate to maths and to find a research question. Do you have any suggestions for me?

hello! im currently struggling on finding my math IA topics and the due date is already getting near. can you please help me and give some guidance?

hi i need help choosing a math ia topic, anything easy and simple will be good please and thank you

i need help in find a IA for math AI HL I'm interested in exercise, dance, business, food

IA idea check

I need help in finding my internal assessment topic, which will be on modeling

I AM FINDING DIFFICUTLY IN SEARCHING IA HL MATH TOPIC. PLZ.HELP

Hello, I want help in math aa IA. I am interested in cooking so please tell me something related to it.

Hello, I am not sure what to choose as a topic for my math IA. I am a standard level student and math is not my strength so something where knowledge of simple maths is enough would be perfect. I am very interested in medicine so something in this area would suit my interest but I don't exactly know how to combine it with maths. Also, maybe math behind billiards but I don't know if this is too complicated for me.

I want to do a AA math IA in Statistics or logarithms but I don't know what topics to do or where to start.

Hey, I need help in finding a maths IA topic. I am interested in cars, technology, and cricket. Could you please help me

Hi I need help with finding a math IA topic. I'm interested in something along the lines of differentiation or volume of revolution. I'm also really interested on the knitting idea mentioned above but could not see how IB math would relate to that. Can you help me out? Thanks.

hey i need help for my math ia

i need help picking a maths IA topic related to zeno's paradox and infinite geometric sequences, I need an example that differs Achilles and the Tortoise. Otherwise a topic in medicine would also be really interesting.

We’ve updated the guide to include example topics to help you get started.

Hello Everyone,

We've updated this guide with 30+ topic ideas in Math IA for SL and HL levels for inspiration. We hope this guide continues to be helpful.

Hi, I really like chess. Do you think I could cerate an IA topic linking chess and math ? Could you help me pls?

Hi, I need help to know which theories or mathematics I could use to know what would be the number and shape necessary to cover a surface with various mosaics and (if possible) without having to break any.

Cracking the Code: How to Avoid These 8 Common IB Math IA Mistakes

As an IB graduate and IB Maths tutor for the past 5 years, I know firsthand how overwhelming it can be for IB students to tackle a complex research paper. And when that paper involves math, the challenge can feel even greater. That’s why in this article, I want to address the top 8 IB Math IA common mistakes that students make. It is imperative that you avoid these mistakes as the Math IA is a critical assignment that is worth 20% of your final math grade.

Through my tutoring experience, I have noticed that certain mistakes occur repeatedly, and I want to provide insights on how to avoid them. However, before delving into specifics, it’s important to acknowledge the anxiety that students feel when receiving feedback on their work. Having gone through the Math IA process myself, I understand the feeling of having your work scrutinized by teachers or tutors. But it’s crucial to recognize that receiving feedback is a normal part of the process, and even the best students get extensive feedback on their work. It’s essential to use feedback constructively to improve your work.

Mathematics is a technical subject that requires careful consideration of the words used. Misrepresenting a concept or misusing technical terms can significantly impact your grade. To avoid common mistakes, students must pay attention to details, read their work aloud, and utilize tools like Grammarly to identify small errors. Communication is also critical in the Math IA, as the exploration must be coherent, well-organized, concise, and comprehensive. In this article, we will highlight some of the common mistakes that students make when completing the Math IA and provide guidance on how to avoid them.

IB Math IA Common Mistake #1: Personal Engagement

One common mistake I often see in assignments is an overemphasis on personal engagement. While personal engagement is worth four marks, there are many misconceptions about how to use it to one’s advantage. It’s crucial to understand how to get personal engagement marks and not rely on cheesy background stories about one’s personal life, loosely related to the research question.

Personal engagement involves proactively showing how you engage in the assignment. This could include collecting your own data, doing something interesting, reflecting on the assignment, conducting preliminary experiments and improving on them, and using maths creatively. It’s essential to take the initiative and show effort in your assignment. You could also try creating a visual representation of your ideas, which could demonstrate your personal engagement.

The main differentiating factor between a three and a four in personal engagement is the wow factor. If your findings are genuinely interesting and add something to the world’s knowledge, that’s when you get the top marks. Avoid presenting basic or intuitive results that don’t mean much.

To succeed in personal engagement, you don’t have to write cheesy stories about your personal life or your relationship with linear regression. All you need to do is put in the effort and show that you have genuinely engaged with the assignment. The try-hard students who show that they tried hard and put effort into the assignment will score well in personal engagement.

Common Mistake #2 & #3: Improper Research Question and Aim

One of the most common mistakes in writing an IB Math IA is having a poorly formulated research question and not outlining the aim of the study properly. To create a well-crafted research question, you should include the variables you plan to measure and the mathematical analysis you intend to use to find the answers you seek. Your research question should neither be too broad nor too narrow, and you must try to strike the right balance between them. For example, a standard format for the research question could be, “What is the best shape for shampoo bottles to maximize their volume to surface area ratio?”

When you do not have a research question, it is essential to have a very specific aim that tells the examiner precisely what you want to do. The aim serves as a roadmap of what you intend to do in your method, and you must not add any extra background information. Your aim should be exactly what you are going to do, such as coding a simulation to demonstrate X, or determining the correlation between X and Y. Avoid using vague phrases like “relationship between them” and “building my understanding,” as they may not convey a clear sense of purpose.

To summarize, your aim should provide a specific roadmap of what you will do, while your research questions should be specific and describe the variables you will be discussing. If you will be doing multiple things, you can explain that in your aim, starting with what you plan to do, followed by what you will do next to achieve your goal. Remember to avoid providing any background information in your aim.

IB Math IA Common Mistake #4: Explanations and Interpretations

A fourth common mistake is forgetting to explain and interpret things. While there is a balance between explaining things and assuming the examiner has a basic understanding of what you are discussing, it is crucial to ensure that you explain and interpret adequately. Sometimes, students explain easy math that is already obvious, while other times, they forget to explain essential concepts. When writing your IB math IA, try to strike a balance and write to a level that is easily understandable by a friend without needing to explain every detail. By avoiding these common mistakes, you can create a well-written Math IA that demonstrates your understanding of the subject matter.

IB Math IA Common Mistake #5: Ugly Looking Equations

One of the most common mistakes that students make when writing their IB Math IA is failing to format their equations properly. It’s important to ensure that your equations look professional and are easy to read. Nice looking equations can make a significant difference in how your work is perceived by your teacher and examiner.

Here are some tips to help you get started:

• Use equation editors: Most word processors, including Google Docs and Word, have built-in equation editors that allow you to create mathematical expressions using various symbols and formatting options. These editors make it easy to create equations that are visually appealing and easy to read.
• Choose the right fonts: When creating equations, it’s important to use a font that is easy to read and looks professional. Avoid using fonts like Arial or Times New Roman for your equations, as they can be difficult to read and make your IA look unprofessional. Instead, use a different font for your equations and variables than your written text, even when they appear within a paragraph.

If you’re not familiar with using equation editors, it may take some practice to get the hang of it. To learn more about how to type equations nicely for your IB math IA, simply search for “how to use equations in Google Docs” or “how to use equations in Word,” and you’ll find plenty of helpful resources to guide you. While the Google Docs equation editor can be a bit challenging to use at first, with some practice, you’ll soon get the hang of it. Don’t be discouraged if it takes a few tries to create the perfect equation. You should experiment with different symbols, formatting options, and fonts until you find a style that works for you. By following these tips, you can make your equations look neat and professional, which will help improve the overall appearance of your math IA.

IB Math IA Common Mistake #6: Graphs

Graphing mistakes.

Another one of the most common mistakes in IB math IA is presenting poorly labeled or formatted graphs. This can negatively impact the presentation of your work and may also lead to the loss of marks. Here are some common mistakes to avoid when graphing your data:

• Improper labeling of axes and units: It is essential to properly label the x-axis and y-axis of your graph and include units. Additionally, uncertainties should be included, especially when measurements are involved. Ensure that you justify how you calculated the uncertainties.
• Inadequate title or caption: Your graph should have a detailed caption that explains what the graph represents and any relevant features. It should also include a title that is meaningful and accurately reflects the content of the graph.
• Inconsistent formatting: The formatting of your graph should be consistent throughout your IA. This includes keeping the same font, gridlines, and color scheme. This consistency ensures that your graphs are easy to read and understand.
• Poor use of space: Avoid leaving blank spaces on your graph. Ensure that your graph fits all the data points, and if necessary, adjust the x-axis or y-axis to accommodate your data.

Including Equations and R-Squared Values

In addition to graphing, it’s also essential to include equations and R-squared values in your IA. Ensure that you present the equations used to derive your results and include the R-squared value on your graph. This helps your readers understand your methodology and provides transparency to your analysis.

Explaining Calculations

When presenting calculations, ensure that you explain how you derived your results. Show examples of your calculations so that your readers can follow your thought process. Remember, the examiner can only see what’s in your IA, so ensure that you include all calculations.

Common Mistake #7: Improper Use of Mathematical Terminology

The next common mistake I often see in IB math IAs is the misuse of technical terms. It can be challenging to spot such mistakes, but it is crucial to avoid them. A lot of errors that I have seen involve a complete misuse of a technical term. For instance, using “causation” when you mean “correlation” or claiming that something is “significant” when you have not done a hypothesis test for it.

Several terms used in our daily language are mathematical terms that may sound strange when used outside of mathematics. Unless you are doing significance testing, which is a mathematical analytical technique in math, you should not use the word “significant” to talk about your results. The word “significant” has a specific meaning in math, and if you use it colloquially when discussing things, it can make it seem like you do not understand your stats correctly.

It is common to see IB math IAs where students throw in math terms without really understanding what they mean. They may do this to sound smart to the examiner, but it is not advisable. Only use a technical term if you genuinely know what it means. Misusing it can be more detrimental than not using it at all. Your math IA should be readable and not confusing to read. Use normal language and technical terms only when necessary.

IB Math IA Common Mistake #8: Poor Copying Technique

The final IB Math IA common mistake that students make when writing their IB Math IA is to use someone else’s methodology without fully understanding what the person did. They may try to apply a specific method of fitting a curve to their data, for instance, by copying the steps directly from another student’s IA. However, this approach can be problematic because the claims and assumptions that work in one person’s IA may not necessarily work in another’s.

While it’s okay to seek inspiration from other IA examples and build off their ideas, it’s important to do additional research on the subject to fully comprehend the methodology being used. Rather than simply copying the steps, take the time to understand the theory behind the methodology, and why it works in that particular context. This will help you to adapt the methodology to your own IA, and avoid making unnecessary errors.

For example, some students who have attempted to use the ordinary least squares method in their IA have encountered difficulties because they did not fully grasp what ordinary least squares was or how it was calculated. They attempted to fit curve without a clear understanding of the underlying concepts, resulting in errors in the calculations and explanations.

To avoid such pitfalls, it’s recommended that you invest ample time in researching and understanding the methodology that you plan to use in your IA. Spend time reading and trying to wrap your head around the concepts you want to explore. This will not only help you to avoid making mistakes but also enable you to score high in your IA.

Remember, while the IB does not expect you to come up with completely original ideas, it does expect you to demonstrate a strong understanding of the concepts you are exploring. So, take inspiration from others’ work, but make sure you understand the methodology behind it before attempting to replicate it.

Final Remarks

If you have any questions or need assistance with your IA, feel free to reach out to us. We offer IB Math tutoring and IA services, and we are happy to help. You can find more information about our services on our IB tutoring page. Good luck with your IAs!

Related Posts

IB Math AASL May 2024 Past Statistics Exam Predictions

In the world of International Baccalaureate (IB) Math, the AASL Math exams hold immense significance, constituting a substantial 80% of…

Step by Step Guide to Writing Level 7 IB Biology IA

I. Introduction A. Brief Overview of IB Biology IA The IB Biology Internal Assessment (IA) is a crucial component of…

IB Economics IA: A Step-By-Step Guide

In the realm of IB Economics, the Internal Assessment (IA) stands as a pivotal challenge for students. Beyond the constraints…

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

IB Math Internal Assessment: Diverse Topics and Detailed Explorations for IB Students

1. exploring the efficiency of solar panels: a mathematical model.

– Mathematics Area : Applications and Interpretation (AI) – Recommended Level : SL – Description : Utilize mathematical modeling to optimize the angle and placement of solar panels for maximum energy efficiency based on geographical location. – Extension for HL or Further Studies : Incorporate variables such as weather patterns and economic cost-benefit analyses to create a more comprehensive model.

2. The Mathematics Behind Cryptographic Algorithms

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level : HL – Description : Investigate the algebraic structures and number theory principles underlying modern cryptographic systems, such as RSA and ECC. – Extension for HL or Further Studies : Explore the computational complexity of cryptographic algorithms and their vulnerabilities to quantum computing attacks. Note : You would need a strong foundation in number theory, modular arithmetic, and abstract algebra to fully explore this topic. Moreover, narrow the focus to one or two cryptographic systems (like RSA or ECC), as investigating too many could become overwhelming within the IA scope.

3. Statistical Analysis of Climate Change Trends Over the Last Century

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: SL – Description: Use statistical methods to analyze temperature data over time, exploring correlations with greenhouse gas concentrations. – Extension for HL or Further Studies: Apply machine learning techniques to predict future climate trends based on historical data. Note : You should be familiar with concepts like correlation, regression, and potentially time-series analysis, depending on the depth of their investigation.

4. Optimizing Traffic Flow: A Study of Intersection Design Using Calculus

Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Apply calculus to model and optimize traffic flow at busy intersections, considering variables such as light timing and lane configurations. – Extension for HL or Further Studies: Integrate urban planning considerations and simulate dynamic traffic patterns using computer software. Note : Real-world traffic is incredibly complex. To create manageable models, you will likely need to make some simplifying assumptions about traffic behavior. Ensure the focus remains on the application of calculus concepts, even if the traffic models themselves are simplified.

5. Modeling the Spread of Infectious Diseases with Differential Equations

Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description : Use differential equations to model the spread of an infectious disease within a population, analyzing the impact of vaccination and social distancing. – Extension for HL or Further Studies : Consider spatial dynamics and movement patterns to model the spread more realistically.

Note : You might benefit from some background on basic epidemiological models (e.g.,  SIR model ) before creating your own more sophisticated versions. Depending on the focus, the IA could be based on real-world disease data or you could simulate disease spread based on their models. Moreover, It’s essential to maintain focus on a specific disease or infection for tractability within the IA word limit.

6. Investigating Patterns in the Fibonacci Sequence and the Golden Ratio

– Mathematics Area: AA & AI – Recommended Level: SL – Description : Explore the appearance of the Fibonacci sequence and the golden ratio in nature, art, and architecture, using sequence and series theory. – Extension for HL or Further Studies : Analyze the convergence properties of sequences and series that define the golden ratio, exploring its mathematical properties in greater depth. Note : The Fibonacci sequence and golden ratio appear frequently in pop culture and sometimes in overly simplified contexts. Go beyond surface-level observations. For SL, emphasize investigating the appearances of these patterns in nature and design, using your mathematical knowledge to analyze and measure. For HL, the focus should be less on ‘finding’ the golden ratio and more on its mathematical properties: limits, convergence, continued fractions, etc.

7. Analyzing the Viability of Investments Using Time Series Analysis

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: HL – Description : Employ time series analysis to evaluate the performance of different investment portfolios over time, considering economic indicators. – Extension for HL or Further Studies: Implement advanced econometric models to forecast future market trends and assess risk. Note : You should be comfortable with core statistical concepts (distributions, hypothesis testing) and time series methods. For a focused IA, select a specific market or a limited number of investment portfolios.

8. The Geometry of Shadows: Analyzing Solar Eclipses

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: SL – Description: Use geometric principles to model solar and lunar eclipses, calculating their paths and durations based on celestial mechanics. – Extension for HL or Further Studies: Incorporate spherical geometry and trigonometry to account for the curvature of the Earth and the moon’s orbit. Note : You will use principles like similarity, angles, ratios, and potentially 3D modeling to understand how eclipses occur. You will delve into celestial mechanics to calculate eclipse paths and durations. For an HL or Further Studies challenge, you can explore the impact of Earth’s curvature by incorporating spherical geometry and trigonometry into their models. Enhancing the analysis with visuals (diagrams, simulations, or even physical models) and leveraging accessible data sources on eclipses will make this a truly engaging exploration of mathematics and astronomy.

9. Evaluating Environmental Sustainability Through Carbon Footprint Analysis

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: SL – Description: Quantify the carbon footprint of various activities or products, using statistical data analysis to assess environmental impact. – Extension for HL or Further Studies: Explore lifecycle analysis to evaluate the total environmental impact from production to disposal. – Note: You will collect and analyze statistical data to calculate the carbon footprint of various activities, products, or even your own lifestyles. You will use mathematical tools to quantify environmental impact, draw conclusions, and potentially offer insights for reducing emissions. HL students could extend this project by incorporating lifecycle analysis. This involves a broader investigation into the total environmental impact of a product, from its creation to its disposal, requiring more sophisticated analysis.

10. The Math Behind Art: Analyzing Fractal Patterns in Nature and Digital Art

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Investigate  fractal  geometry in natural phenomena and digital art, exploring the mathematical principles that generate complex patterns. –  Extension for HL or Further Studies: Apply complex analysis and dynamic systems theory to explore the mathematical underpinnings of fractals and their infinite complexity. – Note: You will delve into the world of fractal geometry, exploring the mathematical rules that create stunningly intricate patterns in nature and digital art. To understand the underlying structure of fractals, you will investigate concepts like recursion, self-similarity, and potentially complex numbers. The suggested extension opens the door to advanced mathematical concepts within complex analysis and dynamic systems, offering a perfect challenge for HL students fascinated by the infinite complexity and self-replicating nature of fractals. The HL extension implies a need for a deeper understanding of complex numbers and potential self-study into dynamic systems.

11. Analyzing Voter Behavior with Game Theory

– Mathematics Area: Applications and Interpretation (AI)

– Recommended Level: SL

– Description: Utilize game theory to analyze strategic voting behavior in elections, considering factors like voter preferences and election systems.

– Extension for HL or Further Studies: Incorporate models of imperfect information and Bayesian updates to analyze how information campaigns and media influence voter behavior. Note : This topic involves applying game theory concepts to understand voter behavior and strategic decision-making in elections. You should be familiar with basic game theory concepts like  Nash equilibrium ,  dominant strategies , and the  Prisoner’s Dilemma . To make the analysis tractable, focus on a specific election or a simplified model of voter preferences and election rules. The suggested HL extension introduces more advanced game theory concepts, such as games of incomplete information and Bayesian updating. This allows for a more nuanced analysis of how voters respond to information and update their beliefs, opening up interesting questions about the role of media and information campaigns in shaping voter behavior. Collecting real-world data on voter preferences and election outcomes can help ground the game-theoretic models in a concrete context.

12. Modeling the Growth of Social Networks

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Apply graph theory to model the growth patterns of online social networks, exploring metrics such as network density and clustering coefficients. – Extension for HL or Further Studies: Use complex network analysis to simulate the spread of information or trends through a social network. – Note: This topic delves into the fascinating world of network science, using graph theory to understand the structure and growth of social networks. You should be comfortable with basic graph theory concepts like nodes, edges, paths, and connectivity. To model network growth, you might explore models like the Barabási-Albert model or the Watts-Strogatz model, which capture key features of real-world networks like preferential attachment and small-world properties. The suggested HL extension takes the analysis further by simulating dynamic processes on networks, such as the spread of information or the adoption of new trends. This requires a deeper understanding of graph algorithms and potentially some programming skills to implement the simulations. Collecting real-world data from social network APIs (if available) or using publicly available network datasets can help validate the models and make the exploration more concrete. Visualizing the networks and their evolution over time can also be a powerful way to communicate the insights from the analysis.

13. The Mathematics of Sports Bracket Predictions

14. optimizing container packing with linear programming.

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: HL – Description: Utilize linear programming to solve the container loading problem, maximizing the use of space while considering constraints like weight and balance. – Extension for HL or Further Studies: Explore three-dimensional packing problems and the use of heuristic algorithms for complex packing scenarios. – Note: This topic tackles a classic optimization problem in logistics and operations research: how to efficiently pack containers to maximize space utilization. To formulate the problem as a linear program, you should be comfortable with defining decision variables, objective functions, and constraints. The basic problem can be modeled as a two-dimensional bin packing problem, where the goal is to minimize the number of containers needed to pack a given set of items. The model can incorporate constraints on item weights, dimensions, and stacking requirements. The suggested HL extension introduces more complex packing scenarios, such as three-dimensional packing or irregular item shapes. These problems often require advanced optimization techniques like integer programming or heuristic algorithms (e.g., genetic algorithms or simulated annealing). Familiarity with optimization software like  CPLEX  or  Gurobi  can be helpful for solving larger instances of the problem. Collaborating with logistics companies or exploring real-world case studies can provide valuable context and data for the project.

15. Exploring the Efficiency of Water Usage in Agriculture through Differential Equations

– Mathematics Area: Analysis and Approaches (AA)

– Recommended Level: HL

– Description: Model water consumption and efficiency in agricultural systems using differential equations to analyze factors affecting water usage.

– Extension for HL or Further Studies: Incorporate climate models and precipitation data to predict future water needs and optimize resource management.

– Note: This topic combines the power of differential equations with the pressing real-world issue of water conservation in agriculture. To model water consumption in agricultural systems, you should be familiar with basic differential equation concepts like initial value problems, equilibrium solutions, and stability analysis. The models can incorporate factors like crop growth, evapotranspiration, and irrigation efficiency. Collecting data on water usage, crop yields, and soil characteristics for specific agricultural systems can help parameterize and validate the models. The suggested HL extension introduces a broader environmental context by linking the water consumption models with climate models and precipitation forecasts. This requires an understanding of how to couple different models and work with large-scale climate datasets. Familiarity with numerical methods for solving differential equations and some programming skills (e.g., in MATLAB or Python) can be helpful for this extension. Collaborating with agricultural experts or environmental scientists can provide valuable insights and ensure the project is grounded in realistic assumptions and data.

16. Analyzing the Impact of Interest Rates on Personal Savings

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: SL – Description: Use exponential growth models to analyze how changes in interest rates affect personal savings and investment strategies over time. – Extension for HL or Further Studies: Explore the effects of inflation and compound interest in varying economic climates to devise optimal saving strategies. – Note: This topic applies mathematical modeling to the personal finance domain, focusing on the impact of interest rates on savings growth. To analyze savings growth, you should be comfortable with exponential functions, logarithms, and the concept of compound interest. The basic model can explore how different interest rates and compounding periods affect the growth of a fixed initial savings amount over time. The analysis can be extended to compare different savings instruments (e.g., savings accounts, CDs, bonds) and their associated interest rates. The suggested HL extension introduces additional economic factors like inflation and varying interest rate environments. This requires an understanding of how to incorporate time-varying parameters into the growth models and how to interpret the results in the context of economic conditions. Researching historical interest rate and inflation data can provide a realistic backdrop for the analysis and help illustrate the importance of considering these factors in long-term savings strategies. Collaborating with financial planners or economists can offer valuable insights into the practical implications of the mathematical models.

17. Modeling the Dynamics of Predator-Prey Populations in an Ecosystem

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Use the  Lotka-Volterra equations  to model the interactions between predator and prey populations, analyzing stability and oscillatory behavior. – Extension for HL or Further Studies: Integrate stochastic elements to simulate environmental variability and its impact on ecosystem dynamics. – Note: This topic explores the fascinating world of population dynamics using the classic Lotka-Volterra equations. To model predator-prey interactions, you should be familiar with systems of differential equations, phase plane analysis, and concepts like equilibrium points and limit cycles. The basic Lotka-Volterra model captures the essentials of predator-prey dynamics, including the cyclical behavior of population sizes. The model can be analyzed mathematically to determine the stability of equilibrium points and the conditions for coexistence of both populations. The suggested HL extension introduces an element of realism by incorporating stochastic factors into the model. This involves understanding how to formulate and simulate stochastic differential equations, which can capture the effects of environmental fluctuations or demographic variability on population dynamics. Familiarity with numerical methods for solving differential equations and programming skills (e.g., in MATLAB or R) can be helpful for this extension. Collaborating with ecologists or wildlife biologists can provide valuable insights into the real-world applicability of the models and the interpretation of the results in the context of conservation and ecosystem management.

18. Investigating the Geometry of Crystals through Symmetry and Group Theory

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Apply principles of symmetry and group theory to analyze the geometric properties of crystals, focusing on lattice structures and symmetry operations. – Extension for HL or Further Studies: Explore the application of X-ray crystallography data in determining crystal structures. – Note: This topic combines the beauty of geometry with the abstract power of group theory to understand the structure of crystals. To analyze crystal symmetries, you should be comfortable with basic group theory concepts like symmetry operations, point groups, and space groups. The project can focus on a specific class of crystals (e.g., cubic or hexagonal) and explore how symmetry operations relate to the physical properties of the crystal. Visualizing crystal structures using 3D modeling software can help develop intuition about the geometric relationships. The suggested HL extension introduces the experimental technique of X-ray crystallography, which is used to determine the atomic structure of crystals. This involves understanding how X-ray diffraction patterns relate to the underlying crystal lattice and how to use mathematical techniques like Fourier analysis to reconstruct the atomic positions. Familiarity with linear algebra and complex numbers can be helpful for this extension. Collaborating with crystallographers or materials scientists can provide valuable insights into the practical aspects of crystal structure determination and the implications for materials design.

19. Optimizing Public Transportation Systems Using Graph Theory

– Description: Analyze public transportation networks using graph theory, optimizing routes and schedules to improve efficiency and reduce transit times.

– Extension for HL or Further Studies: Incorporate real-time data and dynamic routing algorithms to simulate and improve responsive transit systems.

– Note: This topic applies graph theory to the real-world problem of optimizing public transportation systems. To model transportation networks, you should be familiar with graph theory concepts like nodes, edges, paths, and connectivity. The project can focus on a specific transportation mode (e.g., bus or subway) in a particular city and use graph algorithms like shortest path or minimum spanning tree to optimize routes and schedules. Collecting data on transit times, passenger flows, and network topology can help parameterize the models and evaluate the effectiveness of different optimization strategies. The suggested HL extension introduces a dynamic element by incorporating real-time data and responsive routing algorithms. This involves understanding how to update graph models based on changing traffic conditions or passenger demands and how to implement efficient algorithms for real-time route optimization. Familiarity with data structures like priority queues and programming skills (e.g., in Python or Java) can be helpful for this extension. Collaborating with transportation planners or city authorities can provide valuable insights into the practical constraints and objectives of transit system optimization.

20. The Mathematics of Music: Analyzing Harmonic Structures

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: SL – Description: Explore the mathematical relationships between musical notes, scales, and chords, using frequency ratios to understand harmonic structures. – Extension for HL or Further Studies: Apply Fourier analysis to decompose complex musical tones into their constituent frequencies, exploring the mathematical basis of timbre.

– Note: This topic explores the fascinating connections between mathematics and music theory. To analyze harmonic structures, you should be familiar with basic concepts like frequency ratios, intervals, and scales. The project can focus on a specific musical scale (e.g., the equal-tempered scale) and explore how mathematical relationships among frequencies give rise to consonant and dissonant chords. Visualizing musical intervals and chords using tools like the circle of fifths can help illustrate the underlying mathematical patterns. The suggested HL extension introduces the powerful technique of Fourier analysis, which allows complex musical tones to be decomposed into their constituent frequencies. This involves understanding how to represent musical signals as mathematical functions and how to apply Fourier transforms to extract frequency information. Familiarity with trigonometric functions and complex numbers can be helpful for this extension. Collaborating with musicians or music theorists can provide valuable insights into the perceptual aspects of harmony and the practical implications of mathematical music theory.

21. Forecasting Stock Market Trends Using Time Series Analysis

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: HL – Description: Employ time series analysis to forecast stock market trends, utilizing historical price data and indicators. – Extension for HL or Further Studies: Integrate advanced machine learning models, such as ARIMA and LSTM networks, to enhance prediction accuracy and analyze market volatility. – Note: This topic applies time series analysis to the dynamic world of stock market forecasting. To analyze stock market trends, you should be familiar with statistical concepts like autocorrelation, moving averages, and trend decomposition. The project can focus on a specific stock or market index and use historical price data to fit time series models like exponential smoothing or ARIMA. Incorporating external factors like economic indicators or sentiment analysis can help improve the predictive power of the models. The suggested HL extension introduces advanced machine learning techniques specifically tailored for time series data. This involves understanding how to train and validate models like LSTM (Long Short-Term Memory) networks, which can capture complex temporal dependencies in stock prices. Familiarity with programming languages like Python and libraries like TensorFlow or Keras can be helpful for implementing these models. Collaborating with financial analysts or data scientists can provide valuable insights into the practical challenges and considerations of stock market forecasting.

22. The Mathematics of Eco-Friendly Packaging Design

– Description: Use optimization techniques to design eco-friendly packaging that minimizes material usage while maintaining structural integrity.

– Extension for HL or Further Studies: Analyze lifecycle assessment data to optimize packaging design for environmental impact across the entire product lifecycle.

– Note: This topic applies mathematical optimization to the important problem of designing sustainable packaging. To optimize packaging design, you should be familiar with geometric concepts like surface area and volume, as well as basic optimization techniques like linear programming or gradient descent. The project can focus on a specific type of packaging (e.g., boxes or bottles) and explore how to minimize material usage while satisfying constraints related to product protection and structural stability. Incorporating data on material properties and environmental impact can help guide the design process towards more eco-friendly solutions. The suggested HL extension introduces the holistic perspective of lifecycle assessment (LCA), which considers the environmental impact of a product across its entire lifecycle, from raw material extraction to disposal. This involves understanding how to integrate LCA data into the optimization process and how to navigate trade-offs between different environmental objectives (e.g., minimizing carbon footprint vs. maximizing recyclability). Familiarity with multi-objective optimization techniques and sustainability metrics can be helpful for this extension. Collaborating with packaging engineers or environmental scientists can provide valuable insights into the practical considerations and industry standards for sustainable packaging design.

23. Exploring the Fibonacci Sequence in Nature

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: SL – Description: Investigate the occurrence of the Fibonacci sequence in natural phenomena, such as plant growth patterns and animal breeding. – Extension for HL or Further Studies: Apply mathematical models to explore the evolutionary advantages and underlying mechanisms of Fibonacci patterns in nature. Note: This topic explores the fascinating appearance of the Fibonacci sequence in various natural phenomena. To investigate Fibonacci patterns, you should be familiar with the definition and properties of the Fibonacci sequence, as well as basic concepts in geometry and proportions. The project can focus on a specific example of Fibonacci numbers in nature, such as the spiral arrangement of seeds in a sunflower or the branching patterns of trees. Collecting data and measurements from real-world specimens can help validate the presence of Fibonacci patterns and explore their statistical prevalence. The suggested HL extension introduces a more theoretical perspective by considering the evolutionary and mechanistic basis of Fibonacci patterns. This involves understanding how to formulate and analyze mathematical models of plant growth or animal population dynamics that give rise to Fibonacci-like sequences. Familiarity with concepts from mathematical biology, such as L-systems or optimal foraging theory, can be helpful for this extension. Collaborating with biologists or ecologists can provide valuable insights into the biological significance and practical implications of Fibonacci patterns in nature.

24. Optimizing Diet Plans Using Linear Programming for Nutritional Balance

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: HL – Description: Develop a linear programming model to optimize diet plans, ensuring nutritional balance and dietary requirements are met. – Extension for HL or Further Studies: Incorporate stochastic variables to model dietary preferences and restrictions, and use Monte Carlo simulations to analyze various dietary scenarios. – Note: This topic applies linear programming techniques to the practical problem of optimizing diet plans for nutritional balance. To formulate the diet optimization problem, you should be familiar with the basic concepts of linear programming, such as decision variables, objective functions, and constraints. The project can focus on a specific dietary context (e.g., vegetarian diets or athlete nutrition) and use nutritional data on various foods to construct a linear program that minimizes cost or maximizes nutrient intake while satisfying dietary requirements. Incorporating data on individual dietary needs and food preferences can help personalize the optimization results. The suggested HL extension introduces an element of uncertainty by considering dietary preferences and restrictions as stochastic variables. This involves understanding how to formulate and solve stochastic linear programs and how to use Monte Carlo simulations to generate and analyze multiple dietary scenarios. Familiarity with probability distributions and programming skills (e.g., in Python or R) can be helpful for implementing these simulations. Collaborating with nutritionists or dietitians can provide valuable insights into the practical considerations and health implications of optimized diet plans.

25. Modeling Traffic Flow and Congestion using Differential Equations

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Model traffic flow and congestion using differential equations to analyze patterns and propose solutions for reducing traffic jams. – Extension for HL or Further Studies: Implement fluid dynamics models to simulate traffic flow and assess the impact of traffic management strategies. – Note: This topic applies differential equations to model the complex dynamics of traffic flow and congestion. To model traffic, you should be familiar with basic concepts of differential equations, such as initial value problems, equilibrium solutions, and stability analysis. The project can focus on a specific road network or highway section and use traffic data (e.g., vehicle counts, speeds) to formulate and calibrate the differential equation models. Incorporating factors like road capacity, driver behavior, and traffic control strategies can help improve the realism and practical relevance of the models. The suggested HL extension introduces more advanced traffic flow models based on fluid dynamics principles. This involves understanding how to formulate and solve partial differential equations (PDEs) that describe the spatio-temporal evolution of traffic density and velocity. Familiarity with numerical methods for solving PDEs and programming skills (e.g., in MATLAB or Python) can be helpful for implementing these models. Collaborating with traffic engineers or city planners can provide valuable insights into the practical challenges and policy implications of traffic management.

26. The Mathematics of Sustainable Energy Consumption

– Description: Analyze energy consumption data to model sustainable energy usage patterns and assess the impact of renewable energy sources.

– Extension for HL or Further Studies: Use predictive analytics to forecast future energy demands and evaluate the feasibility of various renewable energy projects.

27. Analyzing Sports Performance Using Statistical Models

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: SL – Description: Utilize statistical models to analyze sports performance data, identifying key performance indicators and trends. – Extension for HL or Further Studies: Apply machine learning techniques to develop predictive models for athlete performance and injury risk assessment.   – Note: This topic applies statistical modeling techniques to the exciting world of sports performance analysis. To analyze sports data, you should be familiar with basic statistical concepts like descriptive statistics, correlation, and regression. The project can focus on a specific sport or team and use historical performance data to identify key variables that influence success. Incorporating data visualization techniques can help communicate the insights effectively. The suggested HL extension introduces the power of machine learning to develop predictive models for athlete performance. This involves understanding how to preprocess and feature engineer sports data, as well as how to train and validate models like decision trees, random forests, or neural networks. Familiarity with programming languages like Python and libraries like scikit-learn can be helpful for implementing these models. Collaborating with sports analysts, coaches, or physiologists can provide valuable domain knowledge and ensure the practical relevance of the predictive models.

28. Investigating the Geometry of Soap Bubbles and Minimal Surfaces

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Explore the mathematical principles governing soap bubbles and minimal surfaces, using concepts of surface tension and geometry. – Extension for HL or Further Studies: Employ variational calculus to solve problems related to minimal surfaces and analyze their applications in architecture and materials science. Note : This topic explores the fascinating geometry of soap bubbles and minimal surfaces, which arise from the interplay of surface tension and energy minimization principles. To investigate these structures, you should be familiar with multivariate calculus concepts like partial derivatives, surface integrals, and the divergence theorem. The project can focus on a specific class of minimal surfaces (e.g., catenoids or helicoids) and use mathematical models to analyze their geometric properties and stability. Conducting experiments with soap films and bubbles can provide hands-on insights into the physical realizability of different minimal surface shapes. The suggested HL extension introduces the powerful framework of variational calculus to study minimal surfaces as solutions to optimization problems. This involves understanding how to formulate and solve variational problems using techniques like the Euler-Lagrange equation and the calculus of variations. Familiarity with advanced calculus and functional analysis can be helpful for this extension. Exploring the applications of minimal surfaces in architecture, materials science, or biology can highlight the interdisciplinary relevance of this beautiful mathematical topic. Collaborating with physicists, architects, or materials scientists can provide valuable insights into the practical aspects and engineering challenges of minimal surface design.

29. Modeling the Spread of Rumors in Social Networks

– Description : Use graph theory and probability to model the spread of rumors in social networks, analyzing factors that influence the rate and reach of rumor propagation.

– Extension for HL or Further Studies: Integrate sentiment analysis and machine learning to predict the impact of rumors on public opinion and social behavior. – Note : This topic combines graph theory and probability to model the intriguing phenomenon of rumor spread in social networks. To model rumor propagation, you should be familiar with basic graph theory concepts like nodes, edges, and centrality measures, as well as probability concepts like conditional probability and Markov chains. The project can focus on a specific social network platform and use data on user interactions and message propagation to parameterize the rumor spread models. Incorporating factors like user influence, network topology, and content characteristics can help improve the realism and predictive power of the models. The suggested HL extension introduces the application of sentiment analysis and machine learning techniques to assess the impact of rumors on public opinion. This involves understanding how to preprocess and analyze text data from social media posts, as well as how to train and interpret models like sentiment classifiers or topic models. Familiarity with natural language processing techniques and programming skills (e.g., in Python or R) can be helpful for implementing these analyses. Exploring the ethical implications and potential countermeasures for rumor spread can highlight the societal relevance of this research. Collaborating with social scientists, psychologists, or communication experts can provide valuable insights into the human factors and behavioral aspects of rumor propagation.

30. Exploring the Mathematics of Cryptocurrencies and Blockchain

– Mathematics Area: Analysis and Approaches (AA) – Recommended Level: HL – Description: Investigate the mathematical algorithms underlying cryptocurrencies and blockchain technology, focusing on encryption, consensus algorithms, and transaction verification. – Extension for HL or Further Studies: Analyze the security features of blockchain technology, exploring potential vulnerabilities and the mathematics of cryptographic security measures. Note: This topic delves into the fascinating world of cryptocurrencies and blockchain technology, which rely heavily on advanced mathematical concepts from cryptography and distributed systems. To explore the mathematics of cryptocurrencies, you should be familiar with number theory concepts like prime numbers, modular arithmetic, and public-key cryptography, as well as basic principles of distributed consensus and hash functions. The project can focus on a specific cryptocurrency (e.g., Bitcoin) or blockchain platform and analyze the mathematical foundations of its key components, such as the proof-of-work consensus algorithm or the Elliptic Curve Digital Signature Algorithm (ECDSA) used for transaction signing. Implementing simplified versions of these algorithms can provide hands-on understanding of their mathematical properties. The suggested HL extension introduces a deeper analysis of the security aspects of blockchain technology, which heavily rely on the robustness of the underlying cryptographic primitives. This involves understanding the mathematical principles of cryptographic security, such as computational complexity, one-way functions, and the hardness assumptions underlying specific cryptographic schemes. Familiarity with advanced topics in number theory and cryptography can be helpful for this extension. Exploring the potential vulnerabilities and attack vectors for blockchain systems can highlight the importance of sound mathematical design in ensuring their security and integrity. Collaborating with computer scientists, cryptographers, or blockchain developers can provide valuable insights into the practical implementation challenges and ongoing research in this rapidly evolving field.

31. Mathematics of Image Compression

– Mathematics Area: Applications and Interpretation (AI) – Recommended Level: SL – Description: Explore the use of mathematical algorithms in image compression, focusing on lossless and lossy compression techniques and their effects on image quality and file size. – Extension for HL or Further Studies: Delve into wavelet compression algorithms and their efficiency in compressing different types of images, including medical imaging and high-resolution photographs. – Note: This topic explores the fascinating world of image compression, which relies on sophisticated mathematical algorithms to reduce the size of digital images while maintaining acceptable quality. To investigate image compression techniques, you should be familiar with basic concepts from linear algebra, such as matrices and transformations, as well as discrete mathematics concepts like algorithms and data structures. The project can focus on a specific compression algorithm (e.g., JPEG or PNG) and analyze the mathematical principles behind its encoding and decoding processes, such as the Discrete Cosine Transform (DCT) or the Huffman coding. Implementing simplified versions of these algorithms and comparing their performance on different image types can provide hands-on understanding of their strengths and limitations. The suggested HL extension introduces a more advanced class of compression algorithms based on wavelet transforms, which offer superior performance for certain image types, such as medical images or high-resolution photographs. This involves understanding the mathematical theory of wavelets, including multiresolution analysis and the fast wavelet transform algorithm. Familiarity with signal processing concepts and programming skills (e.g., in MATLAB or Python) can be helpful for implementing and visualizing wavelet-based compression schemes. Exploring the trade-offs between compression ratio and image quality for different application domains can highlight the practical relevance of image compression research. Collaborating with computer scientists, imaging experts, or professionals from fields like medical imaging or remote sensing can provide valuable insights into the real-world challenges and requirements of image compression.

32. Optimizing Airline Flight Schedules with Graph Theory

– Mathematics Area : Analysis and Approaches (AA) – Recommended Level : HL – Description : Use graph theory to optimize airline flight schedules, minimizing layover times and maximizing the efficiency of aircraft utilization. – Extension for HL or Further Studies : Integrate real-time data on weather conditions and airport traffic to dynamically adjust flight schedules for improved efficiency and passenger satisfaction. – Note: This topic applies graph theory to the complex problem of optimizing airline flight schedules, which involves balancing various operational, economic, and passenger satisfaction factors. To model flight networks and optimize schedules, you should be familiar with graph theory concepts like weighted graphs, shortest path algorithms (e.g., Dijkstra’s algorithm), and network flow problems. The project can focus on a specific airline or region and use real-world flight data to construct the graph models and formulate the optimization objectives, such as minimizing total travel time or maximizing aircraft utilization. Incorporating constraints related to aircraft maintenance, crew scheduling, and airport capacity can help improve the realism and practical relevance of the optimization results.

The suggested HL extension introduces a dynamic aspect to flight schedule optimization by considering real-time data on weather conditions and airport congestion. This involves understanding how to update graph models based on changing environmental factors and how to implement efficient algorithms for real-time schedule adjustments. Familiarity with data structures like priority queues and programming skills (e.g., in Python or Java) can be helpful for implementing these dynamic optimization algorithms. Exploring the impact of flight schedule optimization on passenger satisfaction and airline performance metrics can highlight the practical significance of this research.

33. Statistical Analysis of Climate Change Data

– Mathematics Area : Applications and Interpretation (AI) – Recommended Level : SL – Description : Conduct a statistical analysis of climate change data, including temperature trends, sea-level rise, and carbon dioxide concentrations, to model future climate scenarios. – Extension for HL or Further Studies : Apply advanced statistical models, such as multivariate regression and time series analysis, to predict the impact of climate change on specific ecosystems and human populations. – Note: This topic applies statistical analysis techniques to the critical issue of climate change, which has far-reaching environmental, social, and economic consequences. To analyze climate change data, you should be familiar with basic statistical concepts like descriptive statistics, hypothesis testing, and regression analysis. The project can focus on a specific aspect of climate change (e.g., global temperature trends or sea-level rise) and use historical data from reliable sources to identify significant patterns and trends. Visualizing the data using appropriate charts and graphs can help communicate the findings effectively.

The suggested HL extension introduces more advanced statistical modeling techniques to predict the impact of climate change on specific ecosystems or human populations. This involves understanding how to formulate and interpret multivariate regression models that consider multiple climate variables and their interactions. Time series analysis methods, such as ARIMA or SARIMA models, can be used to forecast future climate trends based on historical patterns. Familiarity with statistical software packages like R or Python libraries like statsmodels can be helpful for implementing these advanced analyses.

34. Mathematical Modeling of Human Population Growth

– Mathematics Area : Analysis and Approaches (AA) – Recommended Level : HL – Description : Create mathematical models to predict human population growth, incorporating factors such as birth rates, death rates, and migration patterns. – Extension for HL or Further Studies : Examine the effects of policy interventions, such as family planning and immigration regulations, on population growth trends using differential equations and simulation models. – Note: This topic applies mathematical modeling techniques to the complex dynamics of human population growth, which has significant implications for resource allocation, economic development, and environmental sustainability. To model population growth, you should be familiar with differential equations, particularly first-order and second-order linear and nonlinear equations. The project can focus on a specific country or region and use historical population data to parameterize the models and validate their predictions. Incorporating factors like age structure, fertility rates, and migration flows can help improve the realism and accuracy of the population growth models.

The suggested HL extension introduces a policy analysis dimension by examining the effects of various interventions on population growth trends. This involves understanding how to modify the differential equation models to incorporate the impact of policies like family planning programs, education initiatives, or immigration regulations. Simulation techniques, such as agent-based modeling or system dynamics, can be used to explore the long-term consequences of different policy scenarios. Familiarity with programming languages like Python or specialized modeling software like Stella or NetLogo can be helpful for implementing these simulations.

35. Analyzing Game Strategies using Game Theory

36. mathematics of musical harmony and dissonance.

– Mathematics Area : Analysis and Approaches (AA) – Recommended Level : HL – Description : Investigate the mathematical principles underlying musical harmony and dissonance, examining the ratios of frequencies and their impact on human perception of sound. – Extension for HL or Further Studies : Analyze the construction of musical scales and chords using group theory and explore the mathematical relationship between musical structures and emotional response. – Note: This topic explores the fascinating intersection of mathematics and music theory, which has a rich history dating back to the ancient Greeks. To investigate musical harmony and dissonance, you should be familiar with basic concepts from trigonometry and logarithms, as well as an understanding of frequency ratios and overtones. The project can focus on a specific musical scale or tuning system (e.g., equal temperament or just intonation) and use mathematical analysis to explain the perceived consonance or dissonance of different intervals and chords. Conducting experiments with acoustic instruments or digital audio software can help illustrate the relationship between frequency ratios and harmonic perception.

The suggested HL extension introduces more advanced mathematical concepts from group theory and psychology to analyze the structure and emotional impact of musical scales and chords. This involves understanding how to represent musical pitch classes and intervals as elements of a mathematical group, as well as how to apply group-theoretic operations like transposition and inversion to generate different musical structures. Familiarity with abstract algebra and basic music theory notation can be helpful for this analysis.

37. Optimizing Renewable Energy Production with Calculus

– Mathematics Area : Applications and Interpretation (AI) – Recommended Level : SL – Description : Use calculus to optimize the production of renewable energy sources, such as solar panels and wind turbines, maximizing output while minimizing costs. – Extension for HL or Further Studies : Incorporate environmental impact assessments into the optimization model, evaluating the trade-offs between energy production, cost, and ecological sustainability. – Note: This topic applies calculus techniques to optimize the production of renewable energy sources, which is a critical challenge for transitioning to a more sustainable and low-carbon future. To optimize energy production, you should be familiar with basic calculus concepts like derivatives, integrals, and optimization methods. The project can focus on a specific renewable energy technology (e.g., solar panels or wind turbines) and use calculus to model the relationship between various design parameters and energy output. Collecting data on real-world energy production systems and their associated costs can help validate the optimization results.

The suggested HL extension introduces an environmental impact assessment dimension to the optimization problem, which involves considering the ecological footprint and sustainability implications of renewable energy production. This requires understanding how to incorporate environmental indicators, such as greenhouse gas emissions, land use, or biodiversity impacts, into the mathematical model as additional constraints or objectives. Multi-objective optimization techniques, such as Pareto efficiency analysis or goal programming, can be used to explore the trade-offs between energy production, cost, and environmental sustainability. Familiarity with life cycle assessment methods and environmental economics concepts can be helpful for this analysis.

38. Exploring the Efficiency of Cryptographic Algorithms

– Mathematics Area : Applications and Interpretation (AI) – Recommended Level : HL – Description : Develop differential equation models to describe and analyze traffic flow on road networks, exploring strategies for minimizing congestion and improving traffic management. – Extension for HL or Further Studies : Integrate real-time data from traffic sensors and GPS devices to create dynamic models that adapt to changing traffic conditions and optimize traffic flow in real-time. – Note: This topic applies the powerful tool of differential equations to model and optimize traffic flow on road networks, which is a critical challenge for improving urban mobility and reducing transportation-related emissions. To develop traffic flow models, you should be familiar with ordinary and partial differential equations, as well as basic concepts from fluid dynamics and queueing theory. The project can focus on a specific road network or intersection and use traffic data (e.g., vehicle counts, speeds, and densities) to calibrate and validate the differential equation models. Exploring different traffic scenarios and control strategies, such as traffic light timing or ramp metering, can provide insights into effective congestion management approaches.

The suggested HL extension introduces a real-time optimization dimension to the traffic flow modeling problem, which involves integrating live data from various sensors and devices to create dynamic and adaptive models. This requires understanding how to process and fuse heterogeneous data streams, such as those from loop detectors, cameras, or GPS probes, and how to update the model parameters and control strategies in real-time. Techniques from control theory, such as model predictive control or reinforcement learning, can be used to develop optimization algorithms that can handle the stochastic and time-varying nature of traffic dynamics. Familiarity with programming languages like Python or MATLAB and experience with traffic simulation software can be helpful for implementing these real-time models.

39. Modeling Traffic Flow and Optimization with Differential Equations

– Recommended Level : HL – Description : Develop differential equation models to describe and analyze traffic flow on road networks, exploring strategies for minimizing congestion and improving traffic management. – Extension for HL or Further Studies : Integrate real-time data from traffic sensors and GPS devices to create dynamic models that adapt to changing traffic conditions and optimize traffic flow in real-time. – Note: This topic applies the powerful tool of differential equations to model and optimize traffic flow on road networks, which is a critical challenge for improving urban mobility and reducing transportation-related emissions. To develop traffic flow models, you should be familiar with ordinary and partial differential equations, as well as basic concepts from fluid dynamics and queueing theory. The project can focus on a specific road network or intersection and use traffic data (e.g., vehicle counts, speeds, and densities) to calibrate and validate the differential equation models. Exploring different traffic scenarios and control strategies, such as traffic light timing or ramp metering, can provide insights into effective congestion management approaches.

40. Statistical Analysis of Genetic Data for Disease Prediction

WHERE TO FIND US

Vancouver Office 2030 Marine Drive, North Vancouver, BC, V7P 1V7, Canada Email: [email protected]

Seattle Office 5608 17th Avenue NW, Suite 1578 Seattle, WA 98107, USA Email: [email protected]

Toronto Office 99 Yorkville Avenue Toronto, ON M5R 1C1, Canada Email: [email protected]

Your Ultimate IB Math IA (Internal Assessment) Guide

• Home . 

The article titled “Understanding the IB Math IA” provides valuable insights and guidance for students undertaking the International Baccalaureate (IB) Math Internal Assessment (IA). With a focus on choosing the right IA topic, structuring the IA effectively, collecting and analyzing data, writing a strong report, avoiding common mistakes, seeking feedback and peer review, presenting the IA, and celebrating success, this article offers comprehensive advice to ensure success in completing one’s IA. Written in an academic style that is objective and impersonal, this resource caters to an audience seeking safety by providing clear instructions and strategies for navigating through the IB Math IA process. By following these guidelines outlined in the article, students can enhance their understanding of how to approach their IB Math IA with confidence and achieve excellent results.

Before we start, IB-Pros offers resources and tutors willing to enhance the quality and effectiveness of your IA project.

Key Takeaways

• The IB Math IA requires applying mathematical concepts to real-world scenarios.
• Choosing the right IA topic is a key aspect and factors to consider include relevance, feasibility, and personal interest.
• Collecting reliable and relevant data is crucial for the credibility and validity of findings.
• Using appropriate mathematical models and tools, such as regression analysis and statistical software, helps analyze data accurately.

Table of Contents

Understanding the IB Math IA

The IB Math IA is a comprehensive and rigorous assessment that requires students to apply mathematical concepts and principles to real-world scenarios in order to demonstrate their understanding of the subject. It serves as an opportunity for students to showcase their analytical skills and problem-solving abilities, as well as their ability to communicate mathematical ideas effectively. The IA consists of several components, including a introduction, exploration, analysis, conclusion, and reflection. Students are expected to clearly define the problem they are investigating and develop a coherent argument supported by mathematical evidence.

One key aspect of the IA is the choice of topic. Selecting the right IA topic is crucial as it determines the direction and scope of the investigation. Students should opt for topics that align with their interests and strengths while considering feasibility within a given timeframe. It is important to choose a topic that offers opportunities for applying various mathematical concepts and techniques.

The next section will delve into strategies for selecting an appropriate IA topic without compromising on its relevance or complexity.

Choosing the Right IA Topic

When selecting an IA topic for the IB Math course, it is crucial to carefully consider various factors such as relevance, feasibility, and personal interest. Relevance refers to the topic’s connection to real-world situations or other subjects within the mathematics curriculum. Choosing a relevant IA topic allows students to apply their mathematical knowledge in practical scenarios and develop a deeper understanding of its applications. Feasibility involves ensuring that the chosen topic can be investigated within the given time frame and resources available. It is important to select a topic that can be explored using appropriate mathematical techniques and data sources. Additionally, personal interest plays a significant role in determining the success of an IA project. Selecting a topic that genuinely interests the student will make the research process more enjoyable and motivate them to delve deeper into their investigation.

By considering these factors, students can choose an appropriate IA topic that aligns with their skills, interests, and goals. This thoughtful selection process sets a solid foundation for structuring their IA and producing a high-quality piece of work.

In the subsequent section about ‘structuring your ia,’ students will learn how to organize their chosen IA topic effectively while adhering to specific guidelines provided by the IB Math course.

Read More About:

IB Extended Essay – Step By Step Guide

IB Extended Essay EE Guide

Ultimate Guide For IB Geography IA (Internal Assessment)

Ultimate Guide for IB Global Politics IA

IB History IA Guide

Structuring Your IA

To effectively structure the IA, students should carefully organize their chosen topic while following specific guidelines provided by the IB Math course. Structuring the IA involves several key steps:

• Introduction: Begin by clearly stating the research question and its significance. Provide background information to give context to the topic.
• Methodology: Outline the methods used for data collection and analysis. This includes specifying variables, explaining equations or models utilized, and discussing any assumptions made.
• Results: Present the findings of the study in a clear and organized manner. Use graphs, charts, or tables to illustrate trends or patterns observed in the data.
• Conclusion: Summarize the main findings and discuss their implications. Address any limitations or areas for further research.

By following these steps, students can ensure that their IA is well-structured and coherent. It allows readers to easily follow the logical progression of ideas and understand the purpose of each section. In the subsequent section about ‘tips for effective data collection and analysis,’ students will learn how to gather reliable data and analyze it accurately without compromising safety precautions.

Tips for Effective Data Collection and Analysis

This discussion will focus on the importance of collecting reliable and relevant data, as well as using appropriate mathematical models and tools in order to ensure accurate analysis. Collecting reliable and relevant data is crucial for obtaining meaningful results that can be applied to real-world situations. Using appropriate mathematical models and tools helps to organize and analyze the collected data effectively, while interpreting and analyzing the data accurately allows for valid conclusions to be drawn.

Collecting reliable and relevant data

Collecting reliable and relevant data is crucial in conducting a comprehensive academic investigation to ensure the credibility and validity of the findings. It is important to use language appropriate for an audience that desires safety, as this helps establish trust and confidence in the research process. One way to enhance the engagement of readers is by incorporating a table that presents information clearly and concisely. For instance, a table comparing different sources of data collection methods can be used to highlight their advantages and disadvantages. This not only makes the writing more interesting but also provides readers with a quick reference point for evaluating different approaches. Transitioning into the subsequent section about ‘using appropriate mathematical models and tools,’ it is essential to consider how these models can effectively analyze the collected data to draw meaningful conclusions.

Using appropriate mathematical models and tools

After collecting reliable and relevant data, the next step in an IB Math IA is to use appropriate mathematical models and tools. This involves selecting the most suitable models and techniques to analyze and interpret the collected data accurately. One of the commonly used mathematical tools is regression analysis, which helps identify relationships between variables and make predictions based on the data. Another useful tool is statistical software, such as Excel or Python, which allows for efficient calculations and visualizations. By employing these tools, students can delve deeper into their data sets, uncover hidden patterns or trends, and draw meaningful conclusions. In doing so, they can better understand the significance of their findings and present a comprehensive analysis in their IA report.

Transition: Moving on to interpreting and analyzing your data accurately…

Interpreting and analyzing your data accurately

To ensure an accurate interpretation and analysis of the data, students must carefully consider the relationships between variables and utilize statistical software tools like regression analysis or Excel to uncover hidden patterns or trends. This step is crucial in providing a comprehensive understanding of the data and avoiding any misinterpretations that may lead to erroneous conclusions. By examining the data using appropriate mathematical models and tools, students can identify significant correlations, outliers, or other important features that may impact their analysis. Moreover, by employing objective and impersonal language when presenting their findings, they can effectively communicate their results to an audience that prioritizes safety. With a thorough examination of the data completed, the next section will focus on writing a strong IA report that accurately portrays these findings without bias or personal opinion.

Writing a Strong IA Report

A comprehensive and well-structured IA report contains a clear and logical flow of ideas, enabling the reader to easily follow the reasoning behind the mathematical investigation. To achieve this, it is important to adopt an academic writing style that is objective and impersonal, eliminating personal pronouns. This style of writing creates a sense of professionalism and allows the focus to remain on the mathematical concepts being presented.

When writing an IA report, it is crucial to use language appropriate for an audience that desires safety. Avoiding jargon or technical terms without proper explanation can create confusion and hinder understanding. Instead, strive for clarity by using precise mathematical language while providing clear explanations and examples.

Furthermore, incorporating mathematical concepts and notations into the report strengthens its overall quality. By clearly defining terms, using appropriate symbols, and explaining equations thoroughly, readers can grasp the underlying mathematics more effectively. This ensures that your investigation is accurately communicated and understood.

Incorporating these elements will help you write a strong IA report that effectively presents your ideas in a clear manner. Transitioning into the subsequent section about incorporating mathematical concepts can be done seamlessly by emphasizing the importance of precise definitions and symbols in conveying mathematical ideas accurately.

Incorporating Mathematical Concepts and Notations

This paragraph will discuss the importance of demonstrating a deep understanding of mathematical concepts and using appropriate notations and symbols in calculations. Demonstrating a deep understanding of mathematical concepts is crucial in writing an IA report as it shows the examiner that you have a strong grasp of the subject matter. Additionally, using appropriate notations and symbols in your calculations helps to convey your ideas clearly and effectively. By adhering to these rules, you can ensure that your IA report is written in an academic style that is objective and impersonal.

Demonstrating a deep understanding of mathematical concepts

Achieving a profound comprehension of mathematical concepts is crucial in order to demonstrate a comprehensive understanding of the subject matter. To evoke emotion in the audience, it is important to recognize that gaining such deep knowledge can be both challenging and rewarding. It requires perseverance and dedication, but the sense of accomplishment when mastering complex mathematical ideas can be immensely satisfying. Additionally, developing a strong foundation in mathematical concepts instills confidence and empowers individuals to solve real-world problems with precision and accuracy. This knowledge serves as a safety net, enabling us to make informed decisions based on logical reasoning rather than guesswork or assumptions. By understanding the intricacies of mathematical concepts, we can navigate through calculations effectively and efficiently, using appropriate notations and symbols to convey our findings accurately. Transitioning into the next section about ‘using appropriate notations and symbols in your calculations’, it is essential to consider how these tools enhance clarity and facilitate communication within the realm of mathematics.

Using appropriate notations and symbols in your calculations

To effectively communicate mathematical calculations, it is imperative to employ appropriate notations and symbols that promote clarity and precision. Mathematical notations serve as a universal language in the field, allowing mathematicians to convey complex concepts concisely. Using standardized symbols ensures consistency and facilitates understanding among researchers, educators, and students alike. In addition to promoting accuracy, proper use of notation enhances the professional presentation of mathematical work. It demonstrates a rigorous approach and attention to detail, which are essential qualities in the discipline. Moreover, accurate notation helps prevent errors and misinterpretations that may arise from ambiguous or inconsistent representations. By utilizing appropriate symbols and notations in their calculations, mathematicians ensure effective communication within the field and contribute to the advancement of mathematical knowledge.

Transitioning into examples of successful IA topics…

Examples of Successful IA Topics

Examples of successful IA topics in the field of mathematics can showcase the range and diversity of investigations undertaken by students, offering inspiration and ideas for future projects. One such topic could be exploring the relationship between music and mathematics, analyzing how mathematical concepts are applied in musical compositions. Another interesting IA topic could involve investigating the patterns and properties of prime numbers, delving into their distribution and potential applications in cryptography. Additionally, a student might choose to explore the mathematics behind origami, examining how geometric principles are utilized to create intricate paper structures. Other possibilities include studying fractals and chaos theory, analyzing their mathematical properties and exploring their real-world applications. These examples highlight the vast array of intriguing IA topics that students can choose from when undertaking a math investigation.

In order to excel in these investigations, students may seek resources for IB Math IA help. These resources can provide guidance on choosing a suitable topic, conducting research effectively, using appropriate mathematical notations and symbols, and organizing data accurately. By utilizing these resources effectively, students can enhance their understanding of mathematical concepts while developing essential research skills required for success in their IA project.

Resources for IB Math IA Help

Utilizing available resources can greatly enhance students’ understanding of mathematical concepts and help develop essential research skills required for success in their IB Math IA project. When embarking on the IA journey, students may find themselves seeking additional support and guidance to navigate through the complexities of their chosen topic. Fortunately, there are numerous resources available that can provide valuable assistance.

One such resource is online forums and discussion boards dedicated to IB Math IA. These platforms allow students to connect with others who are also working on their IA projects, providing a space for exchanging ideas, asking questions, and receiving feedback from peers. Additionally, websites such as Khan Academy offer comprehensive video tutorials covering various mathematical topics relevant to the IA.

In addition to online resources, textbooks specifically designed for the IB Mathematics curriculum can be extremely helpful. These textbooks often include worked examples, practice problems, and explanations of key concepts that align with the requirements of the IA.

By taking advantage of these resources, students can deepen their understanding of mathematical concepts and gain insights into effective research methodologies. With a solid foundation in place, they will be better equipped to avoid common mistakes in their IA project while confidently exploring their chosen topic further.

Avoiding Common Mistakes in the IA

A thorough understanding of the IA requirements is crucial in order to avoid common mistakes and ensure a successful project. When working on an IB Math IA, it is important to be aware of potential pitfalls and take steps to avoid them. Here are some common mistakes that students should strive to avoid:

• Lack of clarity: Clearly defining the research question and objectives from the beginning will help maintain focus throughout the project.
• Insufficient data analysis: Properly analyzing and interpreting data is essential for drawing meaningful conclusions. Students should ensure they use appropriate statistical methods and provide clear explanations for their findings.
• Inadequate mathematical rigor: The IA should demonstrate a strong application of mathematical concepts, so it is important to show logical reasoning, accurate calculations, and precise notation.

By being mindful of these potential pitfalls, students can create a solid foundation for their IA. Additionally, seeking feedback from peers or teachers can provide valuable insights and help identify any areas that may need improvement. Taking advantage of opportunities for peer review can enhance the quality of the project by allowing for constructive criticism and suggestions for improvement. This step allows students to refine their work further before final submission.

Getting Feedback and Peer Review

To ensure accuracy and validity in your IB Math IA, it is crucial to seek feedback and engage in a peer review process. This step allows you to gain valuable insights from others who can provide constructive criticism and identify any errors or weaknesses in your work. By obtaining feedback, you have the opportunity to refine your IA and strengthen its overall quality.

When seeking feedback, it is important to approach individuals who possess knowledge and expertise in mathematics or a related field. They can offer guidance on areas that may require improvement or clarification. Peer review is particularly helpful as it allows for multiple perspectives, enhancing the credibility of your research.

Engaging in this process demonstrates a commitment to producing high-quality work while adhering to academic standards. It also promotes an environment of collaboration and continuous learning, which is essential for personal growth.

In the subsequent section about tips for presenting your IA, you will learn how to effectively communicate your findings and showcase the depth of your research.

Tips for Presenting Your IA

One effective way to enhance the presentation of your IB Math IA is by utilizing clear and concise language, allowing your audience to easily understand and appreciate the depth of your research. By using language that is simple yet precise, you can effectively communicate complex mathematical concepts without overwhelming or confusing your audience. This will create a safer environment for them, as they won’t feel intimidated or discouraged from engaging with your work.

To achieve this objective, consider the following tips:

• Simplify technical terms: Avoid jargon or overly complicated terminology. Instead, use everyday language to explain mathematical concepts in a relatable manner.
• Use visuals: Incorporate graphs, charts, and diagrams to visually represent data and illustrate key points. Visual aids can help simplify complex ideas and make them more accessible.
• Provide explanations: Clearly explain any equations or formulas used in your IA so that even those who may not have an extensive background in mathematics can follow along.

By adopting these strategies, you can ensure that your IA presentation is engaging and accessible to all audiences. With clear language and visual aids at hand, you can confidently celebrate the success of your research in the subsequent section about ‘celebrating your success’.

Celebrating Your Success

Achieving a sense of accomplishment in your IB Math IA can be done by reflecting on the successful completion of your research and analysis, highlighting the significance of your findings within the broader context of mathematical exploration. Celebrating your success in this endeavor is crucial to acknowledge the hard work, dedication, and intellectual growth that went into producing a meaningful piece of mathematical investigation.

When presenting your IA, it is important to emphasize the importance of adhering to safety guidelines. By following ethical practices and ensuring that all data collection methods are conducted responsibly, you demonstrate a commitment to maintaining both personal and academic integrity. Discussing any potential risks involved in carrying out the research also helps create an environment that prioritizes safety.

Furthermore, celebrating success means acknowledging not only individual achievements but also recognizing the collective effort put forth by teachers, peers, and educational institutions. It is essential to express gratitude for their support throughout this process.

Celebrating your success in completing your IB Math IA involves reflection on personal accomplishments while considering the wider implications within the field of mathematics. Demonstrating a commitment to safety ensures ethical practices are followed throughout the research journey. Recognizing those who have contributed to your achievement fosters an atmosphere of gratitude and appreciation for collaborative efforts.

Frequently Asked Questions

How many pages should my ib math ia report be.

The length of an IB Math IA report varies, but it is generally recommended to be around 6-12 pages. However, it ultimately depends on the depth and complexity of the topic being researched and discussed.

Is it necessary to include real-life applications of mathematical concepts in my IA?

Including real-life applications of mathematical concepts in an IB Math IA is not necessary, but it can enhance the relevance and practicality of the research. It allows for a deeper understanding and application of mathematical theories in real-world scenarios.

What are some common mistakes that students make in their IA and how can I avoid them?

Common mistakes in IA include not clearly defining the research question, inadequate data analysis, lack of mathematical rigor, and insufficient referencing. To avoid them, students should carefully plan and structure their IA, use appropriate mathematical techniques, analyze data accurately, and cite sources correctly.

Are there any specific formatting or citation guidelines that I should follow in my IA report?

Specific formatting and citation guidelines should be followed in an IA report. These guidelines ensure accuracy, consistency, and proper attribution of sources. Adhering to them demonstrates professionalism and enhances the credibility of the research findings.

How can I effectively incorporate graphs and visual representations of data in my IA?

Effectively incorporating graphs and visual representations of data in an IA involves providing clear labels, appropriate scales, and accurate data representation. This enhances understanding and communication of the information to the desired audience.

In conclusion, the IB Math IA is a crucial component of the International Baccalaureate program. It requires careful planning and execution to choose the right topic, structure the IA effectively, collect and analyze data, write a strong report, and avoid common mistakes. Seeking feedback and peer review can enhance the quality of the IA. Finally, presenting the IA confidently and celebrating one’s success are important steps in completing this academic endeavor successfully.

Add a Comment

Your achievements bring a sense of fulfillment to our hearts

• Why IB Pros
• Tutoring Packages
• Privacy and Policy
• Terms and conditions

2543 Summer Ave Memphis, TN 38112 Shelby County

Free IB Consultation for YOU!

Still Facing Hard Time with

Our Experts Are Here To Help You Schedule a free consultation today!